
【题目】已知![]() ,
,![]() 是曲线
是曲线![]() 上任意一点,动点
上任意一点,动点![]() 满足
满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线交
的直线交![]() 于
于![]() ,
,![]() 两点,过原点
两点,过原点![]() 与点
与点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() ,求证:
,求证:![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知P是圆F1:(x+1)2+y2=16上任意一点,F2(1,0),线段PF2的垂直平分线与半径PF1交于点Q,当点P在圆F1上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)记曲线C与x轴交于A,B两点,M是直线x=1上任意一点,直线MA,MB与曲线C的另一个交点分别为D,E,求证:直线DE过定点H(4,0).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某部门参加职业技能测试的2000名员工中抽取100名员工,将其成绩(满分100分)按照![]() ,
,![]() ,
,![]() ,
,![]() 分成4组,得到如图所示的频率分布直方图.
分成4组,得到如图所示的频率分布直方图.
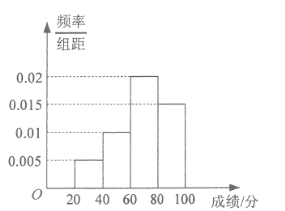
(1)估计该部门参加测试员工的成绩的中位数;
(2)估计该部门参加测试员工的平均成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜花店每天制作![]() 、
、![]() 两种鲜花共
两种鲜花共![]() 束,每束鲜花的成本为
束,每束鲜花的成本为![]() 元,售价
元,售价![]() 元,如果当天卖不完,剩下的鲜花作废品处理.该鲜花店发现这两种鲜花每天都有剩余,为此整理了过往100天这两种鲜花的日销量(单位:束),得到如下统计数据:
元,如果当天卖不完,剩下的鲜花作废品处理.该鲜花店发现这两种鲜花每天都有剩余,为此整理了过往100天这两种鲜花的日销量(单位:束),得到如下统计数据:
| 48 | 49 | 50 | 51 |
天数 | 25 | 35 | 20 | 20 |
| 48 | 49 | 50 | 51 |
天数 | 40 | 35 | 15 | 10 |
以这100天记录的各销量的频率作为各销量的概率,假设这两种鲜花的日销量相互独立.
(1)记该店这两种鲜花每日的总销量为![]() 束,求
束,求![]() 的分布列.
的分布列.
(2)鲜花店为了减少浪费,提升利润,决定调查每天制作鲜花的量![]() 束.以销售这两种鲜花的日总利润的期望值为决策依据,在每天所制鲜花能全部卖完与
束.以销售这两种鲜花的日总利润的期望值为决策依据,在每天所制鲜花能全部卖完与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为4,且过点
的焦距为4,且过点![]() .
.
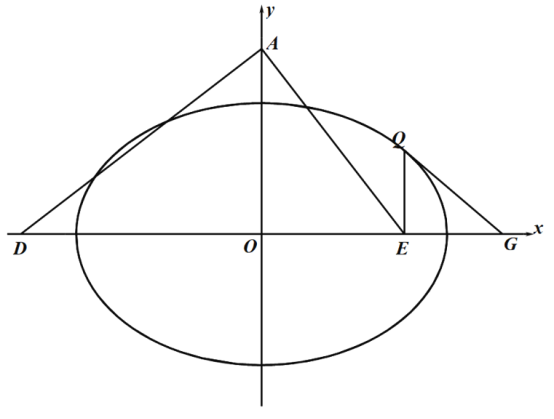
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为椭圆
为椭圆![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,取点
,取点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,作直线
轴的对称点,作直线![]() ,问这样作出的直线
,问这样作出的直线![]() 是否与椭圆
是否与椭圆![]() 一定有唯一的公共点?并说明理由.
一定有唯一的公共点?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com