
【题目】已知定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时, ![]() ,若在
,若在![]() 内关于
内关于![]() 的方程
的方程![]() 恰有3个不同的实数根,则
恰有3个不同的实数根,则![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
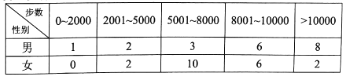
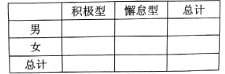
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附: 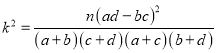 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=x3+ax2+bx+1的导数f′(x)满足f′(1)=2a,f′(2)=﹣b,其中常数a,b∈R. (Ⅰ)求曲线y=f(x)在点(1,f(1))处的切线方程.
(Ⅱ)设g(x)=f′(x)e﹣x . 求函数g(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC 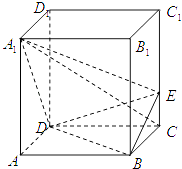
(1)证明:A1C⊥平面BED;
(2)求二面角A1﹣DE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某城市有一块半径为40m的半圆形(以O为圆心,AB为直径)绿化区域,现计划对其进行改建.在AB的延长线上取点D,使OD=80m,在半圆上选定一点C,改建后的绿化区域由扇形区域AOC和三角形区域COD组成,其面积为S m2. 设∠AOC=x rad.
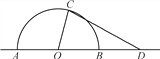
(1)写出S关于x的函数关系式S(x),并指出x的取值范围;
(2)张强同学说:当∠AOC=![]() 时,改建后的绿化区域面积S最大.张强同学的说法正确吗?若不正确,请求出改建后的绿化区域面积S最大值.
时,改建后的绿化区域面积S最大.张强同学的说法正确吗?若不正确,请求出改建后的绿化区域面积S最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读下列结论的证法,再解决后面的问题:已知a1 , a2∈R,a1+a2=1,求证a12+a22≥ ![]() .
.
【证明】构造函数f(x)=(x﹣a1)2+(x﹣a2)2
则f(x)=2x2﹣2(a1+a2)x+a12+a22
=2x2﹣2x+a12+a22
因为对一切x∈R,恒有f(x)≥0.
所以△=4﹣8(a12+a22)≤0,从而得a12+a22≥ ![]() ,
,
(1)若a1 , a2 , …,an∈R,a1+a2+…+an=1,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com