练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知等差数列｛an｝中，a10=5，a13=20，求a50.

    思路解析：通过a10=5和a13=20先求出a1和d，再利用通项公式求a50是基本方法.

    解法一：设数列｛an｝的首项为a1，公差为d，则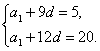

    解得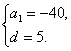

    ∴a50=a1+49d=-40+49×5=205.

    解法二：∵a13=a10+3d，

    ∴d==5.

    所以a50=a10+40d=5+40×5=205.

    解法三：令an=pn+q，

    则解得

    ∴an=5n-45.

    所以a50=5×50-45=205.

    深化升华

    解法二中a13=a10+3d，可以解释为a10是“新”数列的首项，则a13就是该“新”数列的第4项（非第3项）；解法三中an=pn+q是等差数列通项公式的变形式,利用该式解等差数列问题，也是常用方法之一.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知等差数列数﹛an﹜的前n项和为Sn，等比数列﹛bn﹜的各项均为正数，公比是q，且满足：a1=3，b1=1，b2+S2=12，S2=b2q．
    （Ⅰ）求an与bn；
    （Ⅱ）设cn=3bn-λ•2
    an3
    （λ∈R），若﹛cn﹜满足：cn+1＞cn对任意的n∈N°恒成立，求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年周至二中三模理） 已知等差数列｛an｝的公差为2，若a1，a3，a4成等比数列，则a2等于         （    ）

    （A）－4   （B）－6     （C）－8     （D）－10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知等差数列｛an｝的项数n为奇数，且奇数项和S奇＝44，偶数项和S偶＝33，求项数n及数列的中间项.

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年重庆市高三上学期第二次理科数学测试卷（解析版） 题型：选择题

    已知等差数列｛an｝与｛bn｝的前n项和分别为Sn与Tn, 若, 则的值是  

    A.             B.               C.           D.

     

    查看答案和解析>>

    同步练习册答案