Question

用辗转相除法求8 251与6 105的最大公约数,写出算法分析，画出程序框图，写出算法程序.

Answer 1

解：用两数中较大的数除以较小的数，求得商和余数：8 251=6 105×1+2 146.

由此可得，6 105与2 146的公约数也是8 251与6 105的公约数，反过来，8 251与6 105的公约数也是6 105与2 146的公约数，所以它们的最大公约数相等.

对6 105与2 146重复上述步骤：6 105=2 146×2+1 813.

同理，2 146与1 813的最大公约数也是6 105与2 146的最大公约数.继续重复上述步骤：

2 146=1 813×1+333，

1 813=333×5+148，

333=148×2+37，

148=37×4.

    最后的除数37是148和37的最大公约数，也就是8 251与6 105的最大公约数.

    这就是辗转相除法.由除法的性质可以知道，对于任意两个正整数，上述除法步骤总可以在有限步之后完成，从而总可以用辗转相除法求出两个正整数的最大公约数.

算法分析：从上面的例子可以看出，辗转相除法中包含重复操作的步骤，因此可以用循环结构来构造算法.

算法步骤如下：

第一步，给定两个正整数m，n.

第二步，计算m除以n所得的余数为r.

第三步，m=n，n=r.

第四步，若r=0，则m，n的最大公约数等于m；否则，返回第二步.

程序框图如下图：

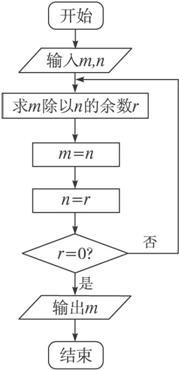
程序：

INPUT  m,n

DO

  r=m MOD n

  m=n

  n=r

LOOP UNTIL r=0

PRINT m

END

点评：从教学实践看，有些学生不能理解算法中的转化过程，例如：求8 251与6 105的最大公约数,为什么可以转化为求6 105与2 146的公约数.因为8 251=6 105×1+2 146，

可以化为8 251-6 105×1=2 164，所以公约数能够整除等式两边的数，即6 105与2 146的公约数也是8 251与6 105的公约数.