
【题目】如图所示的几何体中,正方形![]() 与梯形
与梯形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() .
.
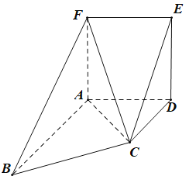
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)取AB中点M,连结MF,MC,可证四边形MCEF为平行四边形,得EC∥MF,进而得证;
(2)由题干面面垂直的性质可得,平面ADEF∩平面ABCD=AD,又AF⊥AD,可证AF⊥平面ABCD,进而得证;
(3)以A为原点,AB,AD,AF所在直线分别为x,y,z轴,建立空间直角坐标系,求出![]() 对应的点坐标,表示出
对应的点坐标,表示出![]() 向量,分别求出平面ABF和平面BCF的法向量,结合向量夹角公式即可求解
向量,分别求出平面ABF和平面BCF的法向量,结合向量夹角公式即可求解
(1)取AB中点M,连结MF,MC,∵MA![]() CD,且MA
CD,且MA![]() CD,∴四边形MCEF为平行四边形,∴EC∥MF,∵EC平面ABF,MF平面ABF,∴EC∥平面ABF.
CD,∴四边形MCEF为平行四边形,∴EC∥MF,∵EC平面ABF,MF平面ABF,∴EC∥平面ABF.
(2)∵平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD, AF⊥AD,AF平面ADEF,∴AF⊥平面ABCD,又∵AF平面FAC,∴平面FAC⊥平面ABCD.
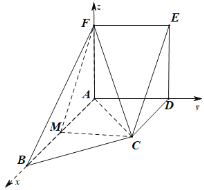
(3)以A为原点,AB,AD,AF所在直线分别为x,y,z轴,建立空间直角坐标系,
则B(4,0,0),F(0,0,2),C(2,2,0),![]() (﹣2,2,0),
(﹣2,2,0),![]() (﹣4,2,0),平面ABF的一个法向量
(﹣4,2,0),平面ABF的一个法向量![]() (0,1,0),设平面BCF的法向量
(0,1,0),设平面BCF的法向量![]() (x,y,z),则
(x,y,z),则 ,取x=1,得
,取x=1,得![]() (1,1,2),设二面角A﹣BF﹣C的平面角为θ,则cosθ
(1,1,2),设二面角A﹣BF﹣C的平面角为θ,则cosθ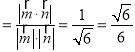 .∴二面角A﹣BF﹣C的余弦值为
.∴二面角A﹣BF﹣C的余弦值为![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】已知棱长为1的正方体![]() ,点
,点![]() 是四边形
是四边形![]() 内(含边界)任意一点,
内(含边界)任意一点,![]() 是
是![]() 中点,有下列四个结论:
中点,有下列四个结论:
①![]() ;②当
;②当![]() 点为
点为![]() 中点时,二面角
中点时,二面角![]() 的余弦值
的余弦值![]() ;③
;③![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ;④当
;④当![]() 时,点
时,点![]() 的轨迹长为
的轨迹长为![]() .
.
其中所有正确的结论序号是( )
A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调研机构,对本地![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,结果显示,有
人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,结果显示,有![]() 人为“低碳族”,该
人为“低碳族”,该![]() 人的年龄情况对应的频率分布直方图如图.
人的年龄情况对应的频率分布直方图如图.

(1)根据频率分布直方图,估计这![]() 名“低碳族”年龄的平均值,中位数;
名“低碳族”年龄的平均值,中位数;
(2)若在“低碳族”且年龄在![]() 、
、![]() 的两组人群中,用分层抽样的方法抽取
的两组人群中,用分层抽样的方法抽取![]() 人,试估算每个年龄段应各抽取多少人?
人,试估算每个年龄段应各抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市一定年龄的市民进行了汉字听写测试.为了调查被测试市民的基本情况,组织方从参加测试的市民中随机抽取120名市民,按他们的年龄分组:第一组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第1组或第4组的概率;
(2)已知第1组市民中男性有3名,组织方要从第1组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性群众的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 和
和![]() 图象的对称轴完全相同,若
图象的对称轴完全相同,若![]() ,则y=g(x)的值域是( )
,则y=g(x)的值域是( )
A. [-1,2] B. [-1,3] C. [,0,2] D. [0,,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为建立健全国家学生体质健康监测评价机制,激励学生积极参加身体锻炼,教育部印发《国家学生体质健康标准(2014年修订)》,要求各学校每学年开展覆盖本校各年级学生的《标准》测试工作.为做好全省的迎检工作,某市在高三年级开展了一次体质健康模拟测试(健康指数满分100分),并从中随机抽取了200名学生的数据,根据他们的健康指数绘制了如图所示的频率分布直方图.

(1)估计这200名学生健康指数的平均数![]() 和样本方差
和样本方差![]() (同一组数据用该组区间的中点值作代表);
(同一组数据用该组区间的中点值作代表);
(2)由频率分布直方图知,该市学生的健康指数![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
①求![]() ;
;
②已知该市高三学生约有10000名,记体质健康指数在区间![]() 的人数为
的人数为![]() ,试求
,试求![]() .
.
附:参考数据![]() ,
,
若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,且椭圆的离心率为
,且椭圆的离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .若直线
.若直线![]() 上存在点P,使得
上存在点P,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,求直线
为顶角的等腰直角三角形,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,若
,若![]() 为
为![]() 的中点.
的中点.
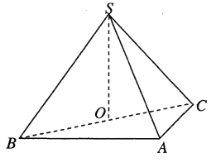
(1)证明:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 和
和![]() 所成角;
所成角;
(3)设线段![]() 上有一点
上有一点![]() ,当
,当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为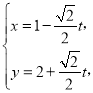 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴为极轴的极坐标系中,圆
轴为极轴的极坐标系中,圆![]() 的方程
的方程![]() .
.
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的直角坐标为
的直角坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求弦
两点,求弦![]() 中点
中点![]() 的直角坐标和
的直角坐标和![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com