
【题目】已知数列{an}满足a1=0,an+1=an+2 ![]() +1
+1
(1)求证数列{ ![]() }是等差数列,并求出an的通项公式;
}是等差数列,并求出an的通项公式;
(2)若bn= ![]() ,求数列{b}的前n项的和Tn .
,求数列{b}的前n项的和Tn .
【答案】
(1)证明:由an+1=an+2 ![]() +1=
+1= ![]() ﹣1,
﹣1,
∴ ![]() ﹣
﹣ ![]() =1,
=1,
故数列{ ![]() }是等差数列,首项为1,公差为1的等差数列.
}是等差数列,首项为1,公差为1的等差数列.
∴ ![]() =1+(n﹣1)
=1+(n﹣1) ![]() =n,
=n,
∴an=n2﹣1
(2)解:bn= ![]() =(n+1)2n,
=(n+1)2n,
∴数列{b}的前n项的和Tn=2×2+3×22+4×23+…+(n+1)2n,
2Tn=2×22+3×23+…+n2n+(n+1)2n+1,
∴﹣Tn=4+22+23+…+2n﹣(n+1)2n+1=2+ ![]() ﹣(n+1)2n+1,
﹣(n+1)2n+1,
可得Tn=n2n+1
【解析】(1)变形利用等差数列的定义与通项公式即可得出.(2)利用“错位相减法”与等比数列的求和公式即可得出.
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系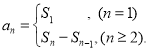 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3ax2﹣9a2x+a3 . 若a> ![]() ,且当x∈[1,4a]时,|f′(x)|≤12a恒成立,则a的取值范围为( )
,且当x∈[1,4a]时,|f′(x)|≤12a恒成立,则a的取值范围为( )
A.( ![]() ,
, ![]() ]
]
B.( ![]() ,1]
,1]
C.[﹣ ![]() ,1]
,1]
D.[0, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经研究发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散.设f(t)表示学生注意力随时间t(分钟)的变化规律(f(t)越大,表明学生注意力越集中),经过实验分析得知:f(t)=  ,
,
(1)求出k的值,并指出讲课开始后多少分钟,学生的注意力最集中?能坚持多久?
(2)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到185,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图,图中四边形是为体现其直观性所作的辅助线.当其主视图和侧视图完全相同时,它的俯视图可能是( ) 
A.
B.
C.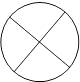
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学根据2002﹣2014年期间学生的兴趣爱好,分别创建了“摄影”、“棋类”、“国学”三个社团,据资料统计新生通过考核远拔进入这三个社团成功与否相互独立,2015年某新生入学,假设他通过考核选拔进入该校的“摄影”、“棋类”、“国学”三个社团的概率依次为m, ![]() ,n,已知三个社团他都能进入的概率为
,n,已知三个社团他都能进入的概率为 ![]() ,至少进入一个社团的概率为
,至少进入一个社团的概率为 ![]() ,且m>n.
,且m>n.
(1)求m与n的值;
(2)该校根据三个社团活动安排情况,对进入“摄影”社的同学增加校本选修字分1分,对进入“棋类”社的同学增加校本选修学分2分,对进入“国学”社的同学增加校本选修学分3分.求该新同学在社团方面获得校本选修课字分分数的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于简单几何体的说法中正确的是( )
①有两个面互相平行,其余各面都是平行四边形的多面体是棱柱;
②有一个面是多边形,其余各面都是三角形的几何体是棱锥;
③在斜二测画法中,与坐标轴不平行的线段的长度在直观图中有可能保持不变;
④有两个底面平行且相似其余各面都是梯形的多面体是棱台;
⑤空间中到定点的距离等于定长的所有点的集合是球面.
A. ③④⑤ B. ③⑤ C. ④⑤ D. ①②⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com