
分析 先作出不等式组所表示的平面区域,由于$\frac{y}{x}$可以看做平面区域内的点与原点的连线的斜率,结合图形可求斜率最大值
解答 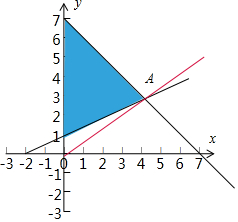 解:作出不等式组所表示的平面区域如图所示:
解:作出不等式组所表示的平面区域如图所示:
由于$\frac{y}{x}$可以看做平面区域内的点与原点的连线的斜率,
结合图形可知,当直线过OA时 斜率最小.
由于$\left\{\begin{array}{l}{x+y=7}\\{x+2=2y}\end{array}\right.$可得A(4,3),此时k=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题主要考查了线性规划在求解最值中的应用,解题的关键是发现所求的式子的几何意义是平面区域内的点与原点的连线的斜率.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:解答题
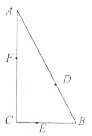 如图,某公园有三条观光大道AB,BC,AC围成直角三角形,其中直角边BC=200m,斜边AB=400m,现有甲、乙、丙三位小朋友分别在AB,BC,AC大道上嬉戏,所在位置分别记为点D,E,F.
如图,某公园有三条观光大道AB,BC,AC围成直角三角形,其中直角边BC=200m,斜边AB=400m,现有甲、乙、丙三位小朋友分别在AB,BC,AC大道上嬉戏,所在位置分别记为点D,E,F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果a1是5的倍数,那么数列{an}与数列{2n}必有相同的项 | |
| B. | 如果a1不是5的倍数,那么数列{an}与数列{2n}必没有相同的项 | |
| C. | 如果a1不是5的倍数,那么数列{an}与数列{2n}只有有限个相同的项 | |
| D. | 如果a1不是5的倍数,那么数列{an}与数列{2n}有无穷多个相同的项. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,分别在x轴与直线$y=\frac{{\sqrt{3}}}{3}({x+1})$上从左向右依次取点Ak、Bk,k=1,2,…,其中A1是坐标原点,使△AkBkAk+1都是等边三角形,则△A10B10A11的边长是512.
如图,在平面直角坐标系中,分别在x轴与直线$y=\frac{{\sqrt{3}}}{3}({x+1})$上从左向右依次取点Ak、Bk,k=1,2,…,其中A1是坐标原点,使△AkBkAk+1都是等边三角形,则△A10B10A11的边长是512.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\sqrt{2},\sqrt{2})$ | B. | $(0,\sqrt{2})$ | C. | $(-\sqrt{2},-\frac{{\sqrt{6}}}{2})∪(\frac{{\sqrt{6}}}{2},\sqrt{2})$ | D. | $(\frac{{\sqrt{6}}}{2},\sqrt{2})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com