
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的极值;
的极值;
(2)当函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,总有
,总有![]() 成立,求整数t的最大值.
成立,求整数t的最大值.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,AD//平面BCC1B1,AD⊥DB.求证:
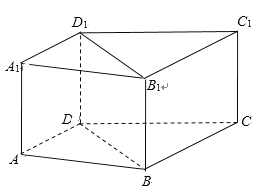
(1)BC//平面ADD1A1;
(2)平面BCC1B1⊥平面BDD1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市新上一种瓶装洗发液,为了打响知名度,举行为期六天的低价促销活动,随着活动的有效开展,第六天该超市对前五天中销售的洗发液进行统计,y表示第x天销售洗发液的瓶数,得到统计表格如下:
x | 1 | 2 | 3 | 4 | 5 |
y | 4 | 6 | 10 | 15 | 20 |
(1)若y与x具有线性相关关系,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ,并预测第六天销售该洗发液的瓶数(按四舍五入取到整数);
,并预测第六天销售该洗发液的瓶数(按四舍五入取到整数);
(2)超市打算第六天加大活动力度,购买洗发液可参加抽奖,中奖者可领取奖金20元,中奖概率为![]() ,已知甲、乙两名顾客抽奖中奖与否相互独立,求甲、乙所获得奖金之和X的分布列及数学期望.
,已知甲、乙两名顾客抽奖中奖与否相互独立,求甲、乙所获得奖金之和X的分布列及数学期望.
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,
,![]() ,M是椭圆E上的一个动点,且
,M是椭圆E上的一个动点,且![]() 的面积的最大值为
的面积的最大值为![]() .
.
(1)求椭圆E的标准方程,
(2)若![]() ,
,![]() ,四边形ABCD内接于椭圆E,
,四边形ABCD内接于椭圆E,![]() ,记直线AD,BC的斜率分别为
,记直线AD,BC的斜率分别为![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
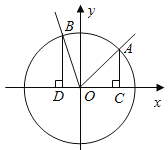
【题目】(本小题满分13分)如图,在直角坐标系![]() 中,角
中,角![]() 的顶点是原点,始边与
的顶点是原点,始边与![]() 轴正半轴重合.终边交单位圆于点
轴正半轴重合.终边交单位圆于点![]() ,且
,且![]() ,将角
,将角![]() 的终边按逆时针方向旋转
的终边按逆时针方向旋转![]() ,交单位圆于点
,交单位圆于点![]() ,记
,记![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)分别过![]() 作
作![]() 轴的垂线,垂足依次为
轴的垂线,垂足依次为![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求角
,求角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的参数方程为
的参数方程为 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到![]() 距离的最大值及该点坐标.
距离的最大值及该点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若函数
,若函数![]() 满足:①在区间
满足:①在区间![]() 上单调递减;②存在常数p,使其值域为
上单调递减;②存在常数p,使其值域为![]() ,则称函数
,则称函数![]() 为
为![]() 的“渐近函数”;
的“渐近函数”;
(1)证明:函数![]() 是函数
是函数![]()
![]() 的渐近函数,并求此时实数p的值;
的渐近函数,并求此时实数p的值;
(2)若函数![]()
![]()
![]() ,证明:当
,证明:当![]() 时,
时,![]() 不是
不是![]() 的渐近函数.
的渐近函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
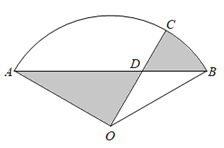
【题目】为响应“生产发展、生活富裕、乡风文明、村容整洁、管理民主”的社会主义新农村建设,某自然村将村边一块废弃的扇形荒地(如图)租给蜂农养蜂、产蜜与售蜜.已知扇形AOB中,![]() ,
,![]() (百米),荒地内规划修建两条直路AB,OC,其中点C在
(百米),荒地内规划修建两条直路AB,OC,其中点C在![]() 上(C与A,B不重合),在小路AB与OC的交点D处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区.设
上(C与A,B不重合),在小路AB与OC的交点D处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区.设![]() ,蜂巢区的面积为S(平方百米).
,蜂巢区的面积为S(平方百米).
(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为何值时,蜂巢区的面积S最小,并求此时S的最小值.
为何值时,蜂巢区的面积S最小,并求此时S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系xOy的原点为极坐标系的极点,x轴的正半轴为极轴.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,P是
,P是![]() 上一动点,
上一动点,![]() ,Q的轨迹为
,Q的轨迹为![]() .
.
(1)求曲线![]() 的极坐标方程,并化为直角坐标方程,
的极坐标方程,并化为直角坐标方程,
(2)若点![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数),直线l与曲线
(t为参数),直线l与曲线![]() 的交点为A,B,当
的交点为A,B,当![]() 取最小值时,求直线l的普通方程.
取最小值时,求直线l的普通方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com