
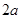 人,(
人,(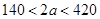 ,且
,且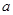 为偶数),每人每年可创利
为偶数),每人每年可创利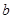 万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利
万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利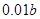 万元,但公司需支付下岗职员每人每年
万元,但公司需支付下岗职员每人每年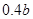 万元的生活费,并且该公司正常运转所需人数不得小于现有员工的
万元的生活费,并且该公司正常运转所需人数不得小于现有员工的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人? 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
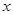 小时的收费为
小时的收费为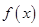 元
元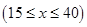 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动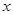 小时的收费为
小时的收费为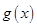 元
元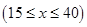 .试求
.试求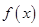 和
和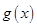 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
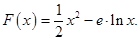
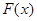 的极值;
的极值;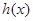 和
和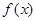 定义域内的任意实数
定义域内的任意实数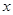 ,若存在常数
,若存在常数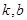 ,使得不等式
,使得不等式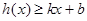 和
和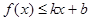 都成立,则称直线
都成立,则称直线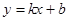 是函数
是函数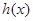 和
和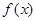 的“分界线”.
的“分界线”.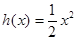 ,
,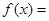
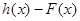 ,试问函数
,试问函数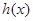 和
和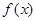 是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
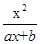 (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.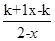 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
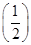 x是R上的1高调函数;
x是R上的1高调函数;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.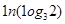 | B.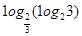 |
C.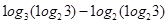 | D.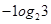 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com