
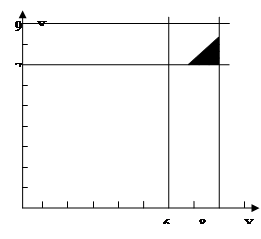
 一个正方形区域,面积为SΩ=4,事件A表示小王离家前不能看到报纸,所构成的区域为A={(X,Y)/
一个正方形区域,面积为SΩ=4,事件A表示小王离家前不能看到报纸,所构成的区域为A={(X,Y)/  即图中的阴影部分,面积为SA=0.5。这是一个几何概型,所以P(A)=SA/SΩ=0.5/4=0.125。
即图中的阴影部分,面积为SA=0.5。这是一个几何概型,所以P(A)=SA/SΩ=0.5/4=0.125。

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源:不详 题型:单选题
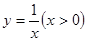 图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为 ( )
图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为 ( )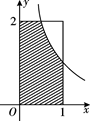
A.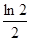 | B.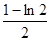 |
C.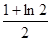 | D.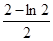 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
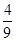 附近,那么点A和点C到直线BD的距离之比约为 .
附近,那么点A和点C到直线BD的距离之比约为 .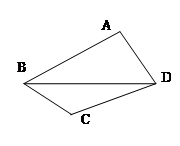
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的圆依次相切,右边正方形内有一个半径为a的内切圆,在这两个图形上各随机撒一粒黄豆,落在阴影内的概率分别为
的圆依次相切,右边正方形内有一个半径为a的内切圆,在这两个图形上各随机撒一粒黄豆,落在阴影内的概率分别为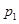 ,
, ,则
,则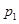 ,
, 的大小关系是:( )
的大小关系是:( )A.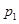 = = | B.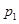 > > | C.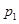 < < | D.无法比较 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com