
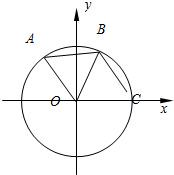
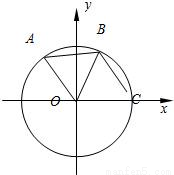
 如图:A,B是圆O上的两点,点C是圆O与x轴正半轴的交点,已知A(-3,4),且点B在劣弧CA上,△AOB为正三角形.
如图:A,B是圆O上的两点,点C是圆O与x轴正半轴的交点,已知A(-3,4),且点B在劣弧CA上,△AOB为正三角形.| x |
| r |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| x |
| r |
| 3 |
| 5 |
| x |
| r |
| 3 |
| 5 |
| y |
| r |
| 4 |
| 5 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
4
| ||
| 10 |
| 3 |
| 3 |
| 15 |
| 5 |


科目:高中数学 来源:2013-2014学年湖北省八市高三下学期3月联考理科数学试卷(解析版) 题型:填空题
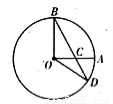
如图,A,B是圆O上的两点,且OA⊥OB,OA=2,C为OA的中点,连接BC并延长交圆O于点D,则CD= .
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省厦门二中高二(上)数学国庆作业4(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2007-2008学年江苏省南京市金陵中学、海安中学高三联考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011年高三数学第一轮基础知识训练(29)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com