
【题目】抖音是一款音乐创意短视频社交软件,是一个专注年轻人的15秒音乐短视频社区,用户可以通过这款软件选择歌曲,拍摄15秒的音乐短视频,形成自己的作品.2018年6月首批25家央企集体入驻抖音,一调研员在某单位进行刷抖音时间的调查,若该单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人.
(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(2)若抽出的7人中有3人是抖音迷,4人为非抖音迷,现从这7人中随机抽取3人做进一步的详细登记.
①用![]() 表示抽取的3人中是抖音迷的员工人数,求随机变量
表示抽取的3人中是抖音迷的员工人数,求随机变量![]() 的分布列与数学期望;
的分布列与数学期望;
②设![]() 为事件“抽取的3人中,既有是抖音迷的员工,也有非抖音迷的员工’’,求事件
为事件“抽取的3人中,既有是抖音迷的员工,也有非抖音迷的员工’’,求事件![]() 发生的概率.
发生的概率.
【答案】(1)应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人;(2)①分布列详见解析,数学期望为![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据分层抽样特征,即可求得各组抽取人数;
(2)由题意,随机变量![]() 所有可能取值为0,1,2,3.根据超几何分布概率求法
所有可能取值为0,1,2,3.根据超几何分布概率求法![]() ,即可求得分布列,进而由期望公式求得数学期望;根据独立事件的加法公式,分类讨论后即可求得事件
,即可求得分布列,进而由期望公式求得数学期望;根据独立事件的加法公式,分类讨论后即可求得事件![]() 发生的概率.
发生的概率.
(1)由已知,甲、乙、丙三个部门的员工人数之比为![]() 由于采用分层抽样的方法从中抽取7人,因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.
由于采用分层抽样的方法从中抽取7人,因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.
(2)①随机变量X的所有可能取值为0,1,2,3.
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
所以,随机变量![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
随机变量X的数学期望![]() .
.
②设事件![]() 为“抽取的3人中,是抖音迷的员工有1人,非抖音迷的员工有2人”;事件
为“抽取的3人中,是抖音迷的员工有1人,非抖音迷的员工有2人”;事件![]() 为“抽取的3人中,是抖音迷的员工有2人,非抖音迷的员工有1人”,则
为“抽取的3人中,是抖音迷的员工有2人,非抖音迷的员工有1人”,则![]() ,且
,且![]() 与
与![]() 互斥,由(Ⅰ)知
互斥,由(Ⅰ)知![]() ,
,
![]() ,
,
故![]() ,
,
所以事件![]() 发生的概率为
发生的概率为![]() .
.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】十五巧板,又称益智图,为清朝浙江省德清知县童叶庚在同治年间所发明,它能拼出草木、花果、鸟兽、鱼虫、文字等图案.十五巧板由十五块板组成一个大正方形(如图1),其中标号为![]() 的小板为等腰直角三角形,图
的小板为等腰直角三角形,图![]() 是用十五巧板拼出的2019年生肖猪的图案,则从生肖猪图案中任取一点,该点恰好取自阴影部分的概率为( )
是用十五巧板拼出的2019年生肖猪的图案,则从生肖猪图案中任取一点,该点恰好取自阴影部分的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过点
,过点![]() 作椭圆C的切线l,在第一象限的切点为P,过点P作与直线l倾斜角互补的直线,恰好经过椭圆C的下顶点N.
作椭圆C的切线l,在第一象限的切点为P,过点P作与直线l倾斜角互补的直线,恰好经过椭圆C的下顶点N.
(1)求椭圆C的方程;
(2)F为椭圆C的右焦点,过点F且与x轴不垂直的直线![]() 交椭圆C于A,B两点,点A关于x轴的对称点为
交椭圆C于A,B两点,点A关于x轴的对称点为![]() ,则直线
,则直线![]() 是否过定点,若是,求出定点坐标;若不是,请说明理由.
是否过定点,若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).以原点
).以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)若直线![]() 与圆
与圆![]() 有公共点,试求实数
有公共点,试求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,过点
时,过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交圆
交圆![]() 于
于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,椭圆![]() 的离心率为
的离心率为![]() ,过点
,过点![]() 作直线
作直线![]() 交椭圆于不同两点
交椭圆于不同两点![]() ,
,![]() .
.
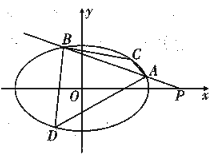
(1)求椭园的方程;
(2)①设直线的斜率为![]() ,求出与直线
,求出与直线![]() 平行且与椭圆相切的直线方程(用
平行且与椭圆相切的直线方程(用![]() 表示);
表示);
②若![]() ,
,![]() 为椭圆上的动点,求四边形
为椭圆上的动点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台![]() 中,
中,![]() ,.若点
,.若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 靠近点
靠近点![]() 的四等分点.
的四等分点.
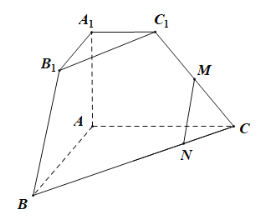
(1)求证:![]() 平面
平面![]() ;
;
(2)若三棱台![]() 的体积为
的体积为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
注:台体体积公式:![]() ,或在
,或在![]() 分别为台体上下底面积,
分别为台体上下底面积,![]() 为台体的高.
为台体的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,平面
的中点,平面![]() 平面
平面![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 平面
平面![]() .
.
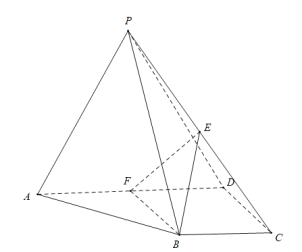
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)(2017·开封二模)为备战某次运动会,某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.
(1)经过备战训练,从6人中随机选出2人进行成果检验,求选出的2人中至少有1个女运动员的概率.
(2)检验结束后,甲、乙两名运动员的成绩用茎叶图表示如图:

计算说明哪位运动员的成绩更稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com