
【题目】已知函数f(x)是定义在R上的奇函数,当x>0时,![]() .
.
(1)求f(x)的解析式;
(2)设x∈[1,2]时,函数![]() ,是否存在实数m使得g(x)的最小值为6,若存在,求m的取值;若不存在,说明理由.
,是否存在实数m使得g(x)的最小值为6,若存在,求m的取值;若不存在,说明理由.
【答案】(1) (2)
(2)![]() .
.
【解析】
(1)设![]() ,根据
,根据![]() 计算
计算![]() ,利用奇偶性即可求解函数解析式;
,利用奇偶性即可求解函数解析式;
(2)通过换元,问题转化为二次函数h (t)在[2, 4]上的最小值为6,再通过分类讨论得出结论.
(1)设![]() ,则
,则![]() ,
,
由当x>0时,![]() 可知,
可知,![]() ,
,
又f(x)为R上的奇函数,
于是![]() ,
,
故当![]() 时,
时,![]() ,
,
当![]() 时,由
时,由![]() 知,
知,![]()
综上知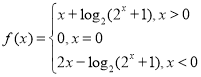
(2)由(1)知,x∈[1,2]时,
![]() ,
,
令![]() ,
,![]() ,
,![]()
函数g(x)的最小值为6,即![]() 在
在![]() 上的最小值为6,
上的最小值为6,
①当![]() ,即m>﹣5时,函数h(t)在[2,4]上为增函数,
,即m>﹣5时,函数h(t)在[2,4]上为增函数,
于是h(t)min=h(2)=6,此时存在满足条件的实数m>﹣5;
②当![]() ,即﹣9≤m≤﹣5时,
,即﹣9≤m≤﹣5时,![]() ,解得
,解得![]() ,此时
,此时![]() 满足条件;
满足条件;
③当![]() ,即m<﹣9时,函数h(t)在[2,4]上为减函数,
,即m<﹣9时,函数h(t)在[2,4]上为减函数,
于是h(t)min=h(4)=2m+20=6,解得![]() ,此时不存在满足条件的实数m;
,此时不存在满足条件的实数m;
综上,存在![]() 使得函数g(x)的最小值为6.
使得函数g(x)的最小值为6.


科目:高中数学 来源: 题型:
【题目】为了缓解市民吃肉难的生活问题,某生猪养殖公司欲将一批猪肉用冷藏汽车从甲地运往相距![]() 千米的乙地,运费为每小时
千米的乙地,运费为每小时![]() 元,装卸费为
元,装卸费为![]() 元,猪肉在运输途中的损耗费(单位:元)是汽车速
元,猪肉在运输途中的损耗费(单位:元)是汽车速![]() 度值的
度值的![]() 倍.(说明:运输的总费用=运费+装卸费+损耗费)
倍.(说明:运输的总费用=运费+装卸费+损耗费)
(1)若汽车的速度为每小时![]() 千米,试求运输的总费用;
千米,试求运输的总费用;
(2)为使运输的总费用不超过![]() 元,求汽车行驶速度的范围;
元,求汽车行驶速度的范围;
(3)若要使运输的总费用最小,汽车应以每小时多少千米的速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为丰富市民的文化生活,市政府计划在一块半径为100m的扇形土地OAB上建造市民广场.规划设计如图:矩形EFGH(其中E,F在圆弧AB上,G,H在弦AB上)区域为运动休闲区,△OAB区域为文化展示区,其余空地为绿化区域,已知P为圆弧AB中点,OP交AB于M,cos∠POB=![]() ,记矩形EFGH区域的面积为Sm2.
,记矩形EFGH区域的面积为Sm2.

(1)设∠POF=θ(rad),将S表示成θ的函数;
(2)求矩形EFGH区域的面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mx2+(1-3m)x-4,m∈R.
(1)当m=1时,求f(x)在区间[-2,2]上的最大值和最小值.
(2)解关于x的不等式f(x)>-1.
(3)当m<0时,若存在x0∈(1,+∞),使得f(x)>0,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂加工一批零件,加工过程中会产生次品,根据经验可知,其次品率![]() 与日产量
与日产量![]() (万件)之间满足函数关系式
(万件)之间满足函数关系式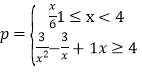 ,已知每生产1万件合格品可获利2万元,但生产1万件次品将亏损1万元.(次品率=次品数/生产量).
,已知每生产1万件合格品可获利2万元,但生产1万件次品将亏损1万元.(次品率=次品数/生产量).
(1)试写出加工这批零件的日盈利额![]() (万元)与日产量
(万元)与日产量![]() (万件)的函数;
(万件)的函数;
(2)当日产量为多少时,可获得最大利润?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 函数
函数![]() 与直线
与直线![]() 相切,设函数
相切,设函数![]() 其中a、c∈R,e是自然对数的底数.
其中a、c∈R,e是自然对数的底数.
(1)讨论h(x)的单调性;
(2)h(x)在区间![]() 内有两个极值点.
内有两个极值点.
①求a的取值范围;
②设函数h(x)的极大值和极小值的差为M,求实数M的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C为锐角三角形ABC的三个内角,若向量![]() =(2-2sinA,cosA+sinA)与向量
=(2-2sinA,cosA+sinA)与向量![]() =(1+sinA,cosA-sinA)互相垂直.
=(1+sinA,cosA-sinA)互相垂直.
(Ⅰ)求角A;
(Ⅱ)求函数y=2sin2B+cos![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全网传播的融合指数是衡量电视媒体在中国网民中影响力的综合指标,根据相关报道提供的全网传播2018年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
组号 | 分组 | 频数 |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
现从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在
内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com