
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.
(1)求椭圆C的方程;
(2)已知直线l:y=kx+ ![]() 与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
【答案】
(1)解:设椭圆的焦半距为c,则由题设,得: 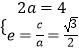 ,
,
解得 ![]() 所以b2=a2﹣c2=4﹣3=1,
所以b2=a2﹣c2=4﹣3=1,
故所求椭圆C的方程为 ![]() +x2=1.
+x2=1.
(2)解:存在实数k使得以线段AB为直径的圆恰好经过坐标原点O.
理由如下:
设点A(x1,y1),B(x2,y2),
将直线l 的方程y=kx+ ![]() 代入
代入 ![]() +x2=1,
+x2=1,
并整理,得(k2+4)x2+2 ![]() kx﹣1=0.(*)
kx﹣1=0.(*)
则x1+x2=﹣ ![]() ,x1x2=﹣
,x1x2=﹣ ![]() .
.
因为以线段AB为直径的圆恰好经过坐标原点O,
所以 ![]() =0,即x1x2+y1y2=0.
=0,即x1x2+y1y2=0.
又y1y2=k2x1x2+ ![]() k(x1+x2)+3,
k(x1+x2)+3,
于是﹣ ![]() ﹣
﹣ ![]() +3=0,解得k=±
+3=0,解得k=± ![]() ,
,
经检验知:此时(*)式的△>0,符合题意.
所以当k=± ![]() 时,以线段AB为直径的圆恰好经过坐标原点O.
时,以线段AB为直径的圆恰好经过坐标原点O.
【解析】(1)设椭圆的焦半距为c,则由题设,得: 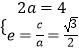 ,解得a,b,c值,可得椭圆C的方程;(2)设点A(x1 , y1),B(x2 , y2),将直线l 的方程y=kx+
,解得a,b,c值,可得椭圆C的方程;(2)设点A(x1 , y1),B(x2 , y2),将直线l 的方程y=kx+ ![]() 代入
代入 ![]() +x2=1,利用韦达定理,及向量垂直的充要条件,可求出满足条件的k值.
+x2=1,利用韦达定理,及向量垂直的充要条件,可求出满足条件的k值.


科目:高中数学 来源: 题型:
【题目】如图,在底面半径和高均为4的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,若过直径CD与点E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为 . 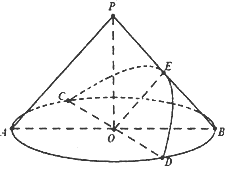
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某几何体的三视图的形状、大小如图所示. 
(1)求该几何体的体积;
(2)设点D、E分别在线段AC、BC上,且DE∥平面ABB1A1 , 求证:DE∥A1B1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥A﹣BCDE中,底面BCDE为平行四边形,平面ABE⊥平面BCDE,AB=AE,DB=DE,∠BAE=∠BDE=90°
(1)求异面直线AB与DE所成角的大小;
(2)求二面角B﹣AE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长春市的“名师云课”活动自开展以来获得广大家长和学子的高度赞誉,在我市推出的第二季名师云课中,数学学科共计推出36节云课,为了更好地将课程内容呈现给广大学子,现对某一时段云课的点击量进行统计:
点击量 |
|
|
|
节数 | 6 | 18 | 12 |
(Ⅰ)现从36节云课中采用分层抽样的方式选出6节,求选出的点击量超过3000的节数.
(Ⅱ)为了更好地搭建云课平台,现将云课进行剪辑,若点击量在区间![]() 内,则需要花费40分钟进行剪辑,若点击量在区间
内,则需要花费40分钟进行剪辑,若点击量在区间![]() 内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中任意取出2节课进行剪辑,求剪辑时间为40分钟的概率.
内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中任意取出2节课进行剪辑,求剪辑时间为40分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为集合A,已知集合B={x|1<x<3},C={x|x≥m},全集为R.
的定义域为集合A,已知集合B={x|1<x<3},C={x|x≥m},全集为R.
(1)求(RA)∩B;
(2)若(A∪B)∩C≠,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对高三年级的学生进行体检,现将高三男生的体重(单位:㎏)数据进行整理后分成五组,并绘制频率分布直方图(如图所示).根据一般标准,高三男生的体重超过65㎏属于偏胖,低于55㎏属于偏瘦,已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25、0.20、0.10、0.05,第二小组的频率数为400,则该校高三年级的男生总数和体重正常的频率分别为( ) 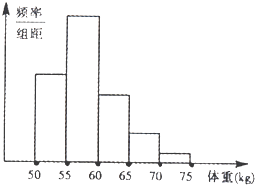
A.1000,0.50
B.800,0.50
C.1000,0.60
D.800,0.60
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于方程(m﹣1)x2+(3﹣m)y2=(m﹣1)(3﹣m),m∈R所表示的曲线C的性状,下列说法正确的是( )
A.对于m∈(1,3),曲线C为一个椭圆
B.m∈(﹣∞,1)∪(3,+∞)使曲线C不是双曲线
C.对于m∈R,曲线C一定不是直线
D.m∈(1,3)使曲线C不是椭圆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(3,1),圆(x﹣1)2+(y﹣2)2=4.
(1)求过M点的圆的切线方程;
(2)若直线ax﹣y+4=0与圆相交于A、B两点,且弦AB的长为2 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com