
分析 (1)由Sn=2an-2(n∈N*),可得a1=2a1-2,解得a1=2;n≥2时,an=Sn-Sn-1,化为:an=2an-1.即可得出.
(2)$\frac{1}{{2}^{n}}$=$\frac{1}{{a}_{n}}$=$\frac{{b}_{1}}{2+1}$-$\frac{{b}_{2}}{{2}^{2}+1}$$+\frac{{b}_{3}}{{2}^{3}+1}$-…+(-1)n+1$\frac{{b}_{n}}{{2}^{n}+1}$,n≥2时,$\frac{1}{{2}^{n-1}}$=$\frac{{b}_{1}}{2+1}$-$\frac{{b}_{2}}{{2}^{2}+1}$$+\frac{{b}_{3}}{{2}^{3}+1}$-…+$(-1)^{n}•\frac{{b}_{n-1}}{{2}^{n-1}+1}$,相减可得:bn=(-1)n$(\frac{1}{{2}^{n}}+1)$.当n=1时,$\frac{{b}_{1}}{3}$=$\frac{1}{2}$,解得b1=$\frac{3}{2}$.
(3)cn=2n+λbn,n≥3时,cn=2n+λ$(-1)^{n}(\frac{1}{{2}^{n}}+1)$,cn-cn-1=2n-1+$(-1)^{n}•λ(2+\frac{3}{{2}^{n}})$>0,即(-1)n•λ>-$\frac{{2}^{n-1}}{\frac{3}{{2}^{n}}+2}$.①当n为大于或等于4的偶数时,λ>-$\frac{1}{\frac{3}{{2}^{2n-1}}+\frac{1}{{2}^{n-2}}}$.②当n为大于或等于3的奇数时,λ<$\frac{1}{\frac{3}{{2}^{2n-1}}+\frac{1}{{2}^{n-2}}}$.当n=2时,c2-c1>0,即λ<8.即可得出.
解答 解:(1)由Sn=2an-2(n∈N*),可得a1=2a1-2,解得a1=2;
n≥2时,an=Sn-Sn-1=2an-2-(2an-1-2),化为:an=2an-1.
∴数列{an}是等比数列,公比为2,首项为2.∴an=2n.
(2)∵$\frac{1}{{2}^{n}}$=$\frac{1}{{a}_{n}}$=$\frac{{b}_{1}}{2+1}$-$\frac{{b}_{2}}{{2}^{2}+1}$$+\frac{{b}_{3}}{{2}^{3}+1}$-…+(-1)n+1$\frac{{b}_{n}}{{2}^{n}+1}$,
∴$\frac{1}{{2}^{n-1}}$=$\frac{{b}_{1}}{2+1}$-$\frac{{b}_{2}}{{2}^{2}+1}$$+\frac{{b}_{3}}{{2}^{3}+1}$-…+$(-1)^{n}•\frac{{b}_{n-1}}{{2}^{n-1}+1}$,
∴$\frac{1}{{2}^{n}}-\frac{1}{{2}^{n-1}}$=(-1)n+1$\frac{{b}_{n}}{{2}^{n}+1}$,∴bn=(-1)n$(\frac{1}{{2}^{n}}+1)$.
当n=1时,$\frac{{b}_{1}}{3}$=$\frac{1}{2}$,解得b1=$\frac{3}{2}$.∴bn=$\left\{\begin{array}{l}{\frac{3}{2},n=1}\\{(-1)^{n}(\frac{1}{{2}^{n}}+1),n≥2}\end{array}\right.$.
(3)cn=2n+λbn,
∴n≥3时,cn=2n+λ$(-1)^{n}(\frac{1}{{2}^{n}}+1)$,cn-1=2n-1+(-1)n-1λ$(\frac{1}{{2}^{n-1}}+1)$,
cn-cn-1=2n-1+$(-1)^{n}•λ(2+\frac{3}{{2}^{n}})$>0,即(-1)n•λ>-$\frac{{2}^{n-1}}{\frac{3}{{2}^{n}}+2}$.
①当n为大于或等于4的偶数时,λ>-$\frac{{2}^{n-1}}{\frac{3}{{2}^{n}}+2}$,即λ>-$\frac{1}{\frac{3}{{2}^{2n-1}}+\frac{1}{{2}^{n-2}}}$,当且仅当n=4时,λ>-$\frac{128}{35}$.
②当n为大于或等于3的奇数时,λ<$\frac{1}{\frac{3}{{2}^{2n-1}}+\frac{1}{{2}^{n-2}}}$,当且仅当n=3时,λ<$\frac{32}{19}$.
当n=2时,c2-c1=$({2}^{2}+\frac{5}{4}λ)$-$(2+\frac{3}{2}λ)$>0,即λ<8.
综上可得:λ的取值范围是$(-\frac{128}{35},\frac{32}{19})$.
点评 本题考查了数列递推关系、等比数列的通项公式、分类讨论方法、不等式的解法、作差法,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | B. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ | D. | $\frac{x^2}{3}-\frac{y^2}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
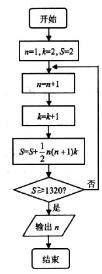 元代数学家朱世杰所著《四元玉鉴》一书,是中国古代数学的重要著作之一,共分卷首、上卷、中卷、下卷四卷,下卷中《果垛叠藏》第一问是:“今有三角垛果子一所,值钱一贯三百二十文,只云从上一个值钱二文,次下层层每个累贯一文,问底子每面几何?”据此,绘制如图所示程序框图,求得底面每边的果子数n为( )
元代数学家朱世杰所著《四元玉鉴》一书,是中国古代数学的重要著作之一,共分卷首、上卷、中卷、下卷四卷,下卷中《果垛叠藏》第一问是:“今有三角垛果子一所,值钱一贯三百二十文,只云从上一个值钱二文,次下层层每个累贯一文,问底子每面几何?”据此,绘制如图所示程序框图,求得底面每边的果子数n为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 温差x(℃) | 13 | 12 | 11 | 10 | 8 |
| 发芽数y(颗) | 30 | 26 | 25 | 23 | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com