
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),坐标原点为极点,
为参数),坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 、
、![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 是曲线
是曲线![]() 上的动点,求
上的动点,求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网络外卖也开始成为不少人日常生活中重要的一部分,其中大学生更是频频使用网络外卖服务.![]() 市教育主管部门为掌握网络外卖在该市各大学的发展情况,在某月从该市大学生中随机调查了
市教育主管部门为掌握网络外卖在该市各大学的发展情况,在某月从该市大学生中随机调查了![]() 人,并将这
人,并将这![]() 人在本月的网络外卖的消费金额制成如下频数分布表(已知每人每月网络外卖消费金额不超过
人在本月的网络外卖的消费金额制成如下频数分布表(已知每人每月网络外卖消费金额不超过![]() 元):
元):
消费金额(单位:百元) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
![]() 由频数分布表可以认为,该市大学生网络外卖消费金额
由频数分布表可以认为,该市大学生网络外卖消费金额![]() (单位:元)近似地服从正态分布
(单位:元)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值,
(每组数据取区间的中点值,![]() ).现从该市任取
).现从该市任取![]() 名大学生,记其中网络外卖消费金额恰在
名大学生,记其中网络外卖消费金额恰在![]() 元至
元至![]() 元之间的人数为
元之间的人数为![]() ,求
,求![]() 的数学期望;
的数学期望;
![]()
![]() 市某大学后勤部为鼓励大学生在食堂消费,特地给参与本次问卷调查的大学生每人发放价值
市某大学后勤部为鼓励大学生在食堂消费,特地给参与本次问卷调查的大学生每人发放价值![]() 元的饭卡,并推出一档“勇闯关,送大奖”的活动.规则是:在某张方格图上标有第
元的饭卡,并推出一档“勇闯关,送大奖”的活动.规则是:在某张方格图上标有第![]() 格、第
格、第![]() 格、第
格、第![]() 格、…、第
格、…、第![]() 格共
格共![]() 个方格.棋子开始在第
个方格.棋子开始在第![]() 格,然后掷一枚均匀的硬币(已知硬币出现正、反面的概率都是
格,然后掷一枚均匀的硬币(已知硬币出现正、反面的概率都是![]() ,其中
,其中![]() ),若掷出正面,将棋子向前移动一格(从
),若掷出正面,将棋子向前移动一格(从![]() 到
到![]() ),若掷出反面,则将棋子向前移动两格(从
),若掷出反面,则将棋子向前移动两格(从![]() 到
到![]() ).重复多次,若这枚棋子最终停在第
).重复多次,若这枚棋子最终停在第![]() 格,则认为“闯关成功”,并赠送
格,则认为“闯关成功”,并赠送![]() 元充值饭卡;若这枚棋子最终停在第
元充值饭卡;若这枚棋子最终停在第![]() 格,则认为“闯关失败”,不再获得其他奖励,活动结束.
格,则认为“闯关失败”,不再获得其他奖励,活动结束.
①设棋子移到第![]() 格的概率为
格的概率为![]() ,求证:当
,求证:当![]() 时,
时,![]() 是等比数列;
是等比数列;
②若某大学生参与这档“闯关游戏”,试比较该大学生闯关成功与闯关失败的概率大小,并说明理由.
参考数据:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月![]() ,
,![]() 两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中
两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中![]() ,
,![]() 两种支付方式都不使用的有5人,样本中仅使用
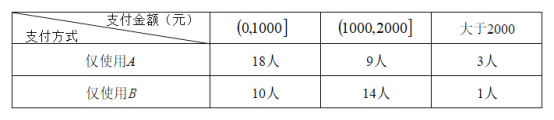
两种支付方式都不使用的有5人,样本中仅使用![]() 和仅使用
和仅使用![]() 的学生的支付金额分布情况如下:
的学生的支付金额分布情况如下:
(1)从全校学生中随机抽取1人,估计该学生上个月![]() ,
,![]() 两种支付方式都使用的概率;
两种支付方式都使用的概率;
(2)从样本仅使用![]() 和仅使用
和仅使用![]() 的学生中各随机抽取1人,以
的学生中各随机抽取1人,以![]() 表示这2人中上个月支付金额大于1000元的人数,求
表示这2人中上个月支付金额大于1000元的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两点![]() ,
,![]() ,给出下列曲线方程:(1)
,给出下列曲线方程:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ,在曲线上存在点
,在曲线上存在点![]() 满足
满足![]() 的所有曲线是( )
的所有曲线是( )
A.(1)(2)(3)(4)B.(2)(3)
C.(1)(4)D.(2)(3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若养殖场每个月生猪的死亡率不超过![]() ,则该养殖场考核为合格,该养殖场在2019年1月到8月养殖生猪的相关数据如下表所示:
,则该养殖场考核为合格,该养殖场在2019年1月到8月养殖生猪的相关数据如下表所示:
月份 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 |
月养殖量/千只3 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 12 |
月利润/十万元 | 3.6 | 4.1 | 4.4 | 5.2 | 6.2 | 7.5 | 7.9 | 9.1 |
生猪死亡数/只 | 29 | 37 | 49 | 53 | 77 | 98 | 126 | 145 |
(1)从该养殖场2019年2月到6月这5个月中任意选取3个月,求恰好有2个月考核获得合格的概率;
(2)根据1月到8月的数据,求出月利润y(十万元)关于月养殖量x(千只)的线性回归方程(精确到0.001).
(3)预计在今后的养殖中,月利润与月养殖量仍然服从(2)中的关系,若9月份的养殖量为1.5万只,试估计:该月利润约为多少万元?
附:线性回归方程![]() 中斜率和截距用最小二乘法估计计算公式如下:
中斜率和截距用最小二乘法估计计算公式如下: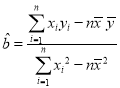 ,
,![]()
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,各项为正的等比数列
为等差数列,各项为正的等比数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() ,__________.在①
,__________.在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选其中一个,补充在横线上,并完成下面问题的解答(如果选择多个条件解答,则以选择第一个解答记分).
这三个条件中任选其中一个,补充在横线上,并完成下面问题的解答(如果选择多个条件解答,则以选择第一个解答记分).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com