
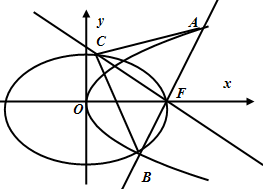
 如图,设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是$\frac{\sqrt{3}}{2}$.
如图,设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是$\frac{\sqrt{3}}{2}$.分析 (1)由已知可得a,又由椭圆C1的离心率得c,b=1即可.
(2)过点F(2,0)的直线l的方程设为:x=my+2,设A(x1,y1),B(x2,y2)联立$\left\{\begin{array}{l}{x=my+2}\\{{y}^{2}=8x}\end{array}\right.$得y2-8my-16=0.|AB|=$\sqrt{1+{m}^{2}}\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$,同理得|CF|=$\sqrt{1+{m}^{2}}|{x}_{c}-{x}_{F}|=\frac{4}{4{m}^{2}+1}$•$\sqrt{1+{m}^{2}}$.△ABC面积s=$\frac{1}{2}$|AB|•|CF|=$\frac{16(1+{m}^{2})}{4{m}^{2}+1}•\sqrt{1+{m}^{2}}$.令$\sqrt{1+{m}^{2}}=t\\;(t≥1)$,则s=f(t)=$\frac{16{t}^{3}}{4{t}^{2}-3}$,利用导数求最值即可.
解答 解:(1)∵椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,∴a=2,
又∵椭圆C1的离心率是$\frac{\sqrt{3}}{2}$.∴c=$\sqrt{3}$,⇒b=1,∴椭圆C1的标准方程:$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(2)过点F(2,0)的直线l的方程设为:x=my+2,设A(x1,y1),B(x2,y2)
联立$\left\{\begin{array}{l}{x=my+2}\\{{y}^{2}=8x}\end{array}\right.$得y2-8my-16=0.
y1+y2=8m,y1y2=-16,∴|AB|=$\sqrt{1+{m}^{2}}\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=8(1+m2).
过F且与直线l垂直的直线设为:y=-m(x-2)
联立$\left\{\begin{array}{l}{y=-m(x-2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$ 得(1+4m2)x2-16m2x+16m2-4=0,
xC+2=$\frac{16{m}^{2}}{1+4{m}^{2}}$,⇒xC=$\frac{2(4{m}^{2}-1)}{4{m}^{2}+1}$.
∴|CF|=$\sqrt{1+{m}^{2}}|{x}_{c}-{x}_{F}|=\frac{4}{4{m}^{2}+1}$•$\sqrt{1+{m}^{2}}$.
△ABC面积s=$\frac{1}{2}$|AB|•|CF|=$\frac{16(1+{m}^{2})}{4{m}^{2}+1}•\sqrt{1+{m}^{2}}$.
令$\sqrt{1+{m}^{2}}=t\\;(t≥1)$,则s=f(t)=$\frac{16{t}^{3}}{4{t}^{2}-3}$,f′(t)=$\frac{16(4{t}^{4}-9{t}^{2})}{(4{t}^{2}-3)^{2}}$,
令f′(t)=0,则t2=$\frac{9}{4}$,即1+m2=$\frac{9}{4}$时,△ABC面积最小.
即当m=±$\frac{\sqrt{5}}{2}$时,△ABC面积的最小值为9,此时直线l的方程为:x=±$\frac{\sqrt{5}}{2}$y+2.
点评 本题考查了直线与椭圆、抛物线的位置关系,考查了运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
 在正方体ABCD-A1B1C1D1中,E,F,G分别为A1B1,BB1,B1C1的中点,则AC1
在正方体ABCD-A1B1C1D1中,E,F,G分别为A1B1,BB1,B1C1的中点,则AC1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,-2,7) | B. | (4,-1,7) | C. | (3,-1,7) | D. | (3,-2,7) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-x | B. | y=log3x | C. | $y={x^{\frac{1}{3}}}$ | D. | y=($\frac{1}{2}$)x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,$BC=EF=\frac{1}{2}AB$,∠BAD=60°,G为BC的中点.
如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,$BC=EF=\frac{1}{2}AB$,∠BAD=60°,G为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 据统计,我国每年交通事故死亡人数已经超过了10万人,我国汽车保有量不到全世界2%,但是交通事故死亡人数则占全球的20%,其中一个很重要的原因是国内很多驾驶员没有养成正确的驾驶习惯,没掌握事故发生前后正确的操作方法.某地交通管理部门从当地某驾校当期一班、二班学员中各随机抽取9名学员参加交通法规知识抽测,测试成绩绘制的茎叶图如下,其中有一个成绩模糊,用x表示.
据统计,我国每年交通事故死亡人数已经超过了10万人,我国汽车保有量不到全世界2%,但是交通事故死亡人数则占全球的20%,其中一个很重要的原因是国内很多驾驶员没有养成正确的驾驶习惯,没掌握事故发生前后正确的操作方法.某地交通管理部门从当地某驾校当期一班、二班学员中各随机抽取9名学员参加交通法规知识抽测,测试成绩绘制的茎叶图如下,其中有一个成绩模糊,用x表示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com