
【题目】已知函数f(x)= 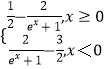
(1)求函数f(x)的零点;
(2)若实数t满足f(log2t)+f(log2 ![]() )<2f(2),求f(t)的取值范围.
)<2f(2),求f(t)的取值范围.
【答案】
(1)解:当x<0时,解 ![]() 得:x=ln
得:x=ln ![]() =﹣ln3,
=﹣ln3,
当x≥0时,解 ![]() 得:x=ln3,
得:x=ln3,
故函数f(x)的零点为±ln3
(2)解:当x>0时,﹣x<0,
此时f(﹣x)﹣f(x)= ![]() =
= ![]() =0,
=0,
故函数f(x)为偶函数,
又∵x≥0时,f(x)= ![]() 为增函数,
为增函数,
∴f(log2t)+f(log2 ![]() )<2f(2)时,2f(log2t)<2f(2),
)<2f(2)时,2f(log2t)<2f(2),
即|log2t|<2,
﹣2<log2t<2,
∴t∈( ![]() ,4)
,4)
故f(t)∈( ![]() ,
, ![]() )
)
【解析】(1)分类讨论,函数对应方程根的个数,综合讨论结果,可得答案.(2)分析函数的奇偶性和单调性,进而可将不等式化为|log2t|<2,解得f(t)的取值范围.


科目:高中数学 来源: 题型:
【题目】为了调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
男 | 女 | 总计 | |
需要帮助 | 40 | m | 70 |
不需要帮助 | n | 270 | s |
总计 | 200 | t | 500 |
(1)求m,n,s,t的值;
(2)估计该地区老年人中,需要志愿者提供帮助的比例;
(3)能否有99%的把握认为该地区的老年人是否需要志愿者帮助与性别有关.
参考公式:
随机变量K2= ![]() ,n=a+b+c+d
,n=a+b+c+d
在2×2列联表:
y1 | y2 | 总计 | |
x1 | a | b | a+b |
x2 | c | d | c+d |
总计 | a+c | b+d | a+b+c+d |
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数y=f(x)对任意x都满足f(x+1)=﹣f(x),且当0≤x<1时,f(x)=x,则函数g(x)=f(x)﹣ln|x|的零点个数为个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级体育课举行了一次“投篮比赛”活动,为了了解本次投篮比赛学生总体情况,从中抽取了甲乙两个小组样本分数的茎叶图如图所示.
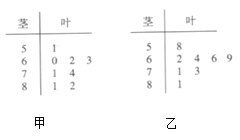
(1)分别求出甲乙两个小组成绩的平均数与方差,并判断哪一个小组的成绩更稳定:
(2)从甲组成绩不低于60分的同学中,任意抽取3名同学,设![]() 表示所抽取的3名同学中得分在
表示所抽取的3名同学中得分在![]() 的学生个数,求
的学生个数,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
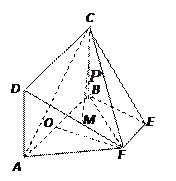
【题目】如图,矩形ABCD所在的平面和平面![]() 互相垂直,等腰梯形
互相垂直,等腰梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点,
的中点, ![]() 为底面
为底面![]() 的重心.
的重心.
(Ⅰ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com