已知函数f(x)=x3+bx2+cx+d(x∈R),f′(0)=6设F(x)=f(x)-f′(x)若F(0)=0,F(1)=-11.
(1)求b、c、d的值.
(2)求F(x)的单调区间与极值.
解:(1)∵f(x)=x
3+bx
2+cx+d,∴f'(x)=3x
2+2bx+c.
由f′(0)=6得c=6,
从而F(x)=f(x)-f'(x)=x
3+bx
2+cx+d-(3x
2+2bx+c)=x
3+(b-3)x
2+(c-2b)x+d-c.
由于F(0)=0,F(1)=-11,
所以d-c=0,且(b-3)+(c-2b)+d-c=-11,
得b=14,c=6,d=6;
(2)由(1)知F(x)=x
3+11x
2-22x,从而F'(x)=3x
2+22x-22,
当F'(x)>0时,x<
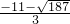
或x>

,
当F'(x)<0时,
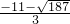
<x<

,
由此可知,(-∞,
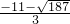
)和(

,+∞)是函数F(x)的单调递增区间;
(
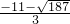
,

)是函数F(x)的单调递减区间;
F(x)在x=
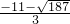
时取得极大值,极大值为369,F(x)在x=

时取得极小值,极小值为-10.
分析:(1)根据F(x)=f(x)-f'(x)且F(0)=0,F(1)=-11,列方程组能够求出b、c与d的值.
(2)对F(x)进行求导,F'(x)>0时的x的取值区间为单调递增区间,F'(x)<0时的x的取值区间为单调递减区间.F'(x)=0时的x,使得函数F(x)取到极值.
点评:本题主要考查对导数的理解.导数大于0时可求原函数的单调递增区间,导数小于0时可求原函数的单调递减区间,取到极值时导数为0.

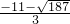 或x>
或x> ,
,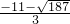 <x<
<x< ,
,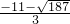 )和(
)和( ,+∞)是函数F(x)的单调递增区间;
,+∞)是函数F(x)的单调递增区间;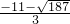 ,
, )是函数F(x)的单调递减区间;
)是函数F(x)的单调递减区间;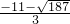 时取得极大值,极大值为369,F(x)在x=
时取得极大值,极大值为369,F(x)在x= 时取得极小值,极小值为-10.
时取得极小值,极小值为-10.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<