
【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知报名的选手情况统计如下表:
组别 | 男 | 女 | 总计 |
中年组 |
|
| 91 |
老年组 | 16 |
|
|
已知中年组女性选手人数是仅比老年组女性选手人数多2人,若对中年组和老年组分别利用分层抽样的方法抽取部分报名者参加比赛,已知老年组抽取了5人,其中女性3人,中年组抽取了7人.
(1)求表格中的数据![]() ;
;
(2)若从选出的中年组的选手中随机抽取两名进行比赛,求至少有一名女性选手的概率.
【答案】(Ⅰ)见解析(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)由题意,老年组中,女性抽取了3人,则男性抽取了2人,利用分层抽样的比例,即可求解![]() 的值;
的值;
(Ⅱ)由已知得中年组抽取男性![]() 人;女性2人,列举出基本事件的个数,利用古典概型的概率计算公式,即可求解至少有一名女性的概率.
人;女性2人,列举出基本事件的个数,利用古典概型的概率计算公式,即可求解至少有一名女性的概率.
试题解析:
(Ⅰ)由题意,老年组中,女性抽取了3人,则男性抽取了2人,故抽样比为![]() .
.
所以![]() .
.
故![]() .
.
所以![]() ,
,![]() .
.
(Ⅱ)由已知,中年组共抽取了7人,所以抽样比为![]() .
.
所以中年组抽取男性![]() 人;女性2人.
人;女性2人.
记5名男性分别为![]() ,2名女性分别为
,2名女性分别为![]() .
.
则从中随机选取两名,不同的结果为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
共21种.
其中至少有一名女性的选法为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .共11种.
.共11种.
所以至少有一名女性的概率为![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
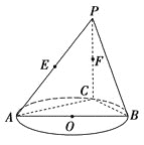
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设AB=PC=2,BC=1,求三棱锥P-BEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为零的等差数列{an}中,a1=1且a1 , a3 , a9成等比数列, (Ⅰ)求数列{an}的通项公式
(Ⅱ)设bn=n2 ![]() 求数列[bn}的前n项和Sn .
求数列[bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如图所示.食堂某天购进了 90个面包,以![]() (个)(其中
(个)(其中![]() )表示面包的需求量,
)表示面包的需求量, ![]() (元)表示利润.
(元)表示利润.
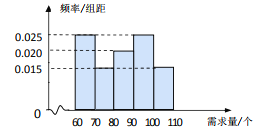
(1)根据直方图计算需求量的中位数;
(2)估计利润![]() 不少于100元的概率;
不少于100元的概率;
(3)在直方图的需求量分组中,以需求量落入该区间的频率作为需求量在该区间的概率,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为
=1(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为 ![]() b.
b.
(1)求椭圆C的离心率;
(2)设b=2,直线y=kx+4与椭圆C交于不同的两点M,N,求证:直线BM与直线AN的交点G在定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ![]() ,中奖可以获得2分;方案乙的中奖率为P0(0<P0<1),中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品. (Ⅰ)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为
,中奖可以获得2分;方案乙的中奖率为P0(0<P0<1),中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品. (Ⅰ)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为 ![]() ,求P0;
,求P0;
(Ⅱ)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装着标有数字1、2、3、4、5的小球各2个,从袋中任取3个小球,每个小球被取出的可能性都相等,用ξ表示取出的3个小球上的最大数字,求:
(1)取出的3个小球上的数字互不相同的概率;
(2)随机变量ξ的概率分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com