
【题目】已知函数f(x)=x2+ ![]() .
.
(1)判断f(x)的奇偶性并说明理由;
(2)当a=16时,判断f(x)在x∈(0,2]上的单调性并用定义证明;
(3)试判断方程x3﹣2016x+16=0在区间(0,+∞)上解的个数并证明你的结论.
【答案】
(1)解:f(x)的定义域为{x|x≠0},关于原点对称.
①a=0时,f(﹣x)=x2=f(x),∴f(x)是偶函数.
②a≠0时,f(﹣x)≠±f(x),∴f(x)是非奇非偶函数
(2)解:当a=16时,f(x)=x2+ ![]() ,任取0<x1<x2≤2,
,任取0<x1<x2≤2,
则f(x1)﹣f(x2)= ![]() ﹣
﹣ ![]() =(x1﹣x2)
=(x1﹣x2) ![]() ,
,
∵0<x1<x2≤2,∴x1﹣x2<0,0<x1x2<4,0<x1+x2<4.
∴(x1﹣x2) ![]() >0,即f(x1)﹣f(x2)>0,∴f(x1)>f(x2).
>0,即f(x1)﹣f(x2)>0,∴f(x1)>f(x2).
∴f(x)在x∈(0,2]上是单调递减函数
(3)解:结论:方程在(0,+∞)上共有两个解.
证明:当a=16时,任取2≤x1<x2,则同理可证f(x1)<f(x2).
∴f(x)在[2,+∞)上是单调递增函数.
∴x3﹣2016x+16=0在的解即为方程x2+ ![]() ﹣2016=0,x∈(0,+∞)的解.
﹣2016=0,x∈(0,+∞)的解.
令g(x)=f(x)﹣2016,
∴当x∈(0,2)时,由 ![]() =16000+
=16000+ ![]() >2016得
>2016得 ![]() >0.
>0.
且f(2)=12<2016得g(2)<0,
又g(x)的图象在x∈(0,2]的解上是不间断的曲线,由零点存在定理知函数在x∈[0,2]上有一个零点,又由g(x)在x∈(0,2]上是单调递减函数,所以函数在[0,2]上只有一个零点.
当x∈(2,+∞)时,由f(2)=12<2016,且f(1000)>0且f(x)在x∈[2,+∞)上是单调递增函数得g(2)<0,
g(1000)>0,g(x)的图象在(2,+∞)上是不间断的曲线,
由零点存在定理知函数在x∈[2,+∞)有一个零点,又由g(x)在x∈(2,+∞)调递增知函数在x∈(2,+∞)只有一个零点
【解析】(1)对a分类讨论,计算f(﹣x)与±f(x)的关系即可判断出奇偶性.(2)当a=16时,f(x)=x2+ ![]() ,任取0<x1<x2≤2,作差f(x1)﹣f(x2)=(x1﹣x2)
,任取0<x1<x2≤2,作差f(x1)﹣f(x2)=(x1﹣x2) ![]() ,判断符号即可证明.(3)利用函数的单调性、函数零点判定定理即可得出.
,判断符号即可证明.(3)利用函数的单调性、函数零点判定定理即可得出.
【考点精析】本题主要考查了函数单调性的判断方法和函数的奇偶性的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;偶函数的图象关于y轴对称;奇函数的图象关于原点对称才能正确解答此题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】孝感市及周边地区的市民游玩又添新去处啦!孝感熙凤水乡旅游度假区于2017年10月1日正式对外开放.据统计,从2017年10月1日到10月7日参观孝感市熙凤水乡旅游度假区的人数如表所示:
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数(万) | 11 | 13 | 8 | 9 | 7 | 8 | 10 |
(1)把这7天的参观人数看成一个总体,求该总体的众数和平均数(精确到0.1);
(2)用简单随机抽样方法从10月1日到10月4日中抽取2天,它们的参观人数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过1万的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,且过点
,且过点![]() .直线
.直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求![]() 的面积的最大值;
的面积的最大值;
(Ⅲ)设直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .判断
.判断![]() ,
, ![]() 大小关系,并加以证明.
大小关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() 的面积的3倍.
的面积的3倍.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 与
与![]() 轴垂直,
轴垂直,![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的动点,且满足
两侧的动点,且满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨< ![]() )的部分图象如图所示,则f(x)的解析式为( )
)的部分图象如图所示,则f(x)的解析式为( ) 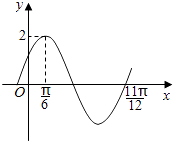
A.f(x)=2sin(x+ ![]() )
)
B.f(x)=2sin(2x+ ![]() )
)
C.f(x)=2sin(2x﹣ ![]() )
)
D.f(x)=2sin(4x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题
(1)在等比数列{an}中,a5=162,公比q=3,前n项和Sn=242,求首项a1和项数n.
(2)有四个数,其中前三个数成等比数列,其积为216,后三个数成等差数列,其和为36,求这四个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com