
ЁОЬтФПЁПдквЛДЮГщбљЕїВщжаВтЕУбљБОЕФ6зщЪ§ОнЃЌЕУЕНвЛИіБфСП![]() Йигк
Йигк![]() ЕФЛиЙщЗНГЬФЃаЭЃЌЦфЖдгІЕФЪ§жЕШчЯТБэЃК
ЕФЛиЙщЗНГЬФЃаЭЃЌЦфЖдгІЕФЪ§жЕШчЯТБэЃК
| 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
(1)ЧыгУЯрЙиЯЕЪ§![]() МгвдЫЕУї
МгвдЫЕУї![]() гы
гы![]() жЎМфДцдкЯпадЯрЙиЙиЯЕ(ЕБ
жЎМфДцдкЯпадЯрЙиЙиЯЕ(ЕБ![]() ЪБЃЌЫЕУї
ЪБЃЌЫЕУї![]() гы
гы![]() жЎМфОпгаЯпадЯрЙиЙиЯЕ)ЃЛ
жЎМфОпгаЯпадЯрЙиЙиЯЕ)ЃЛ
(2)ИљОн(1)ЕФХаЖЯНсЙћЃЌНЈСЂ![]() Йигк
Йигк![]() ЕФЛиЙщЗНГЬВЂдЄВтЕБ
ЕФЛиЙщЗНГЬВЂдЄВтЕБ![]() ЪБЃЌЖдгІЕФ
ЪБЃЌЖдгІЕФ![]() жЕЮЊЖрЩй(
жЕЮЊЖрЩй(![]() ОЋШЗЕН
ОЋШЗЕН![]() ).
).
ИНВЮПМЙЋЪНЃКЛиЙщЗНГЬ![]() жааБТЪКЭНиОрЕФзюаЁЖўГЫЗЈЙРМЦЙЋЪНЗжБ№ЮЊЃК
жааБТЪКЭНиОрЕФзюаЁЖўГЫЗЈЙРМЦЙЋЪНЗжБ№ЮЊЃК
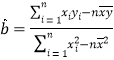 ЃЌ
ЃЌ![]() ЃЌЯрЙиЯЕЪ§
ЃЌЯрЙиЯЕЪ§![]() ЙЋЪНЮЊЃК
ЙЋЪНЮЊЃК .
.
ВЮПМЪ§ОнЃК
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.

| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЯђСП ![]() =ЃЈ1ЃЌЉ3ЃЉЃЌ
=ЃЈ1ЃЌЉ3ЃЉЃЌ ![]() =ЃЈЉ2ЃЌmЃЉЃЌЧв
=ЃЈЉ2ЃЌmЃЉЃЌЧв ![]() ЁЭЃЈ
ЁЭЃЈ ![]() Љ
Љ ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ1ЃЉЧѓЪЕЪ§mЕФжЕЃЛ
ЃЈ2ЃЉЕБk ![]() +
+ ![]() гы
гы ![]() Љ
Љ ![]() ЦНааЪБЃЌЧѓЪЕЪ§kЕФжЕЃЎ
ЦНааЪБЃЌЧѓЪЕЪ§kЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкФГИлПк![]() ДІЛёЯЄ,Цфе§ЖЋЗНЯђОрРы20n mileЕФ
ДІЛёЯЄ,Цфе§ЖЋЗНЯђОрРы20n mileЕФ![]() ДІгавЛЫвгцДЌгіЯеЕШД§гЊОШ,ДЫЪБОШдЎДЌдкИлПкЕФФЯЦЋЮї30ЁуОрИлПк10n mileЕФCДІ,ОШдЎДЌНгЕНОШдЎУќСюСЂМДДгCДІбижБЯпЧАЭљBДІгЊОШгцДЌ.
ДІгавЛЫвгцДЌгіЯеЕШД§гЊОШ,ДЫЪБОШдЎДЌдкИлПкЕФФЯЦЋЮї30ЁуОрИлПк10n mileЕФCДІ,ОШдЎДЌНгЕНОШдЎУќСюСЂМДДгCДІбижБЯпЧАЭљBДІгЊОШгцДЌ.

ЃЈ1ЃЉЧѓНгЕНОШдЎУќСюЪБОШдЎДЌОргцДЌЕФОрРы;
ЃЈ2ЃЉЪдЮЪОШдЎДЌдкCДІгІГЏББЦЋЖЋЖрЩйЖШЕФЗНЯђбижБЯпЧАЭљBДІОШдЎ?ЃЈвбжЊ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЃЈЦфжа
ЃЌЃЈЦфжа![]() ЮЊ
ЮЊ![]() дкЕу
дкЕу![]() ДІЕФЕМЪ§ЃЌ
ДІЕФЕМЪ§ЃЌ ![]() ЮЊГЃЪ§).
ЮЊГЃЪ§).
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈ3ЃЉЩшКЏЪ§![]() ЃЌШєКЏЪ§
ЃЌШєКЏЪ§![]() дкЧјМф
дкЧјМф![]() ЩЯЕЅЕїЕндіЃЌЧѓЪЕЪ§
ЩЯЕЅЕїЕндіЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЁЃ
ЕФШЁжЕЗЖЮЇЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫФИіНсТлЃК
ЂйШєІСЁЂІТЮЊЕквЛЯѓЯоНЧЃЌЧвІСЃОІТЃЌдђsinІСЃОsinІТ
ЂкКЏЪ§y=|sinx|гыy=|tanx|ЕФзюаЁе§жмЦкЯрЭЌ
ЂлКЏЪ§fЃЈxЃЉ=sinЃЈx+ ![]() ЃЉдк[Љ
ЃЉдк[Љ ![]() ЃЌ
ЃЌ ![]() ]ЩЯЪЧдіКЏЪ§ЃЛ
]ЩЯЪЧдіКЏЪ§ЃЛ
ЂмШєКЏЪ§fЃЈxЃЉ=asinxЉbcosxЕФЭМЯѓЕФвЛЬѕЖдГЦжсЮЊжБЯпx= ![]() ЃЌдђa+b=0ЃЎ
ЃЌдђa+b=0ЃЎ
Цфжае§ШЗНсТлЕФађКХЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ ![]() .
.
ЃЈЂёЃЉжЄУїЃК ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЖМВЛЪЧЧњЯп
ЖМВЛЪЧЧњЯп![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈЂђЃЉШє![]() ЃЌЪЙ
ЃЌЪЙ![]() ГЩСЂЃЌЧѓЪЕЪ§
ГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌШ§Ртжљ![]() ЕФЕзУцЪЧБпГЄЮЊ2ЕФе§Ш§НЧаЮЧвВрРтДЙжБгкЕзУцЃЌВрРтГЄЪЧ
ЕФЕзУцЪЧБпГЄЮЊ2ЕФе§Ш§НЧаЮЧвВрРтДЙжБгкЕзУцЃЌВрРтГЄЪЧ![]() ЃЌ
ЃЌ ![]() ЪЧ
ЪЧ![]() ЕФжаЕу.
ЕФжаЕу.
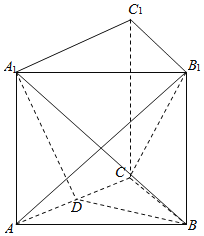
ЃЈ1ЃЉЧѓжЄЃК ![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓЖўУцНЧ![]() ЕФДѓаЁЃЛ
ЕФДѓаЁЃЛ
ЃЈ3ЃЉЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕ.
ЫљГЩНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФРтжљ![]() жаЃЌ
жаЃЌ![]() ЕзУц
ЕзУц![]() ЃЌЕзУц
ЃЌЕзУц![]() ЪЧЬнаЮЃЌ
ЪЧЬнаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉЧѓжЄЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкЯпЖЮ![]() ЩЯЪЧЗёДцдквЛЕу
ЩЯЪЧЗёДцдквЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЦНУц
ЦНУц![]() ЃЌШєДцдкЃЌЧыШЗЖЈЕу
ЃЌШєДцдкЃЌЧыШЗЖЈЕу![]() ЕФЮЛжУЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФЮЛжУЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЕФНЙЕуЮЊ
ЕФНЙЕуЮЊ![]() ЃЌзМЯпЮЊ
ЃЌзМЯпЮЊ![]() ЃЌХзЮяЯпЩЯвЛЕу
ЃЌХзЮяЯпЩЯвЛЕу![]() ЕФКсзјБъЮЊ1ЃЌЧвЕННЙЕу
ЕФКсзјБъЮЊ1ЃЌЧвЕННЙЕу![]() ЕФОрРыЮЊ2.
ЕФОрРыЮЊ2.
ЃЈ1ЃЉЧѓХзЮяЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЩш![]() ЪЧХзЮяЯпЩЯвьгкдЕу
ЪЧХзЮяЯпЩЯвьгкдЕу![]() ЕФСНИіВЛЭЌЕуЃЌжБЯп
ЕФСНИіВЛЭЌЕуЃЌжБЯп![]() КЭ
КЭ![]() ЕФЧуаБНЧЗжБ№ЮЊ
ЕФЧуаБНЧЗжБ№ЮЊ![]() КЭ
КЭ![]() ЃЌЕБ
ЃЌЕБ![]() БфЛЏЧв
БфЛЏЧв![]() ЮЊЖЈжЕ
ЮЊЖЈжЕ![]() ЪБЃЌжЄУїжБЯп
ЪБЃЌжЄУїжБЯп![]() КуЙ§ЖЈЕуЃЌВЂЧѓГіИУЖЈЕуЕФзјБъ.
КуЙ§ЖЈЕуЃЌВЂЧѓГіИУЖЈЕуЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com