
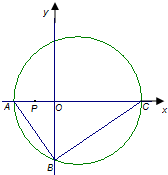
 如图,直角三角形ABC的顶点坐标A(-2,0),直角顶点$B(0,-2\sqrt{2})$,顶点C在x轴上,点P为线段OA的中点.
如图,直角三角形ABC的顶点坐标A(-2,0),直角顶点$B(0,-2\sqrt{2})$,顶点C在x轴上,点P为线段OA的中点.分析 (Ⅰ)求出${k_{BC}}=\frac{{\sqrt{2}}}{2}$,运用直线方程的点斜式列式,再化简即可得到直线BC方程;
(Ⅱ)根据A、C两点的坐标算出AC中点M坐标为(1,0),而圆M的半径R=$\frac{1}{2}$|AC|=3,利用圆方程的标准形式即可写出圆M的方程为(x-1)2+y2=9.
解答 解:(Ⅰ)∵${k_{AB}}=-\sqrt{2}$,(2分)
∴${k_{BC}}=\frac{{\sqrt{2}}}{2}$; (4分)
∴直线BC的方程是y=$\frac{\sqrt{2}}{2}$x-2$\sqrt{2}$﹒(7分)
(Ⅱ)由(Ⅰ)可得C(4,0),(9分)
∴圆心M(1,0),(11分)
∴圆M的方程是:(x-1)2+y2=9﹒(14分)
点评 本题在坐标系中给出Rt△ABC,求直线BC方程,并求△ABC外接圆M方程.着重考查了直线的斜率、直线的方程和圆的标准方程等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
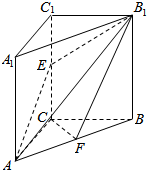 已知在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=1,BC=2,AA1=4.当E为CC1中点时,
已知在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=1,BC=2,AA1=4.当E为CC1中点时,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{9}$,+∞) | B. | [$\frac{1}{3}$,+∞) | C. | (-∞,$\frac{1}{9}$] | D. | (-∞,$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
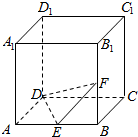 如图,正方体ABCD-A1B1C1D1中,E,F分别为AB与BB1的中点.
如图,正方体ABCD-A1B1C1D1中,E,F分别为AB与BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com