
 ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击. (2) X的分布列为
(2) X的分布列为| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P |  | 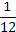 |  |  |  |  |
 ,P(C)=P(D)=
,P(C)=P(D)= ,
,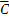
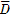 )∪(
)∪(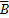 C
C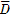 )∪(
)∪(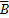
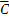 D),
D),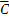
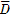 )∪(
)∪(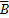 C
C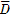 )∪(
)∪(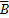
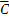 D))=P(B
D))=P(B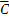
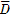 )+P(
)+P(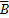 C
C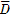 )+P(
)+P(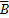
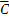 D)
D)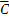 )P(
)P(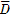 )+P(
)+P(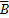 )P(C)P(
)P(C)P(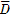 )+P(
)+P(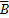 )P(
)P(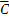 )P(D)
)P(D) ×(1-
×(1- )×(1-
)×(1- )+(1-
)+(1- )×
)× ×(1-
×(1- )+(1-
)+(1- )×(1-
)×(1- )×
)× =
= .
.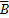
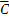
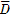 )
) )×(1-
)×(1- )×(1-
)×(1- )=
)=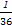 ,
,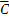
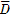 )=P(B)P(
)=P(B)P(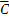 )P(
)P(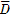 )
) ×(1-
×(1- )×(1-
)×(1- )
)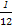 ,
,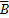 C
C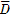 ∪
∪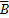
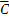 D)=P(
D)=P(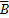 C
C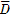 )+P(
)+P(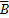
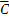 D)
D) )×
)× ×(1-
×(1- )+(1-
)+(1- )×(1-
)×(1- )×
)×
 ,
,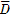 ∪B
∪B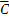 D)=P(BC
D)=P(BC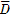 )+P(B
)+P(B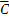 D)
D) ×
× ×(1-
×(1- )+
)+ ×(1-
×(1- )×
)×
 ,
,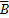 CD)
CD) )×
)× ×
×
 ,
, ×
× ×
×
 .
.| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P |  | 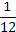 |  |  |  |  |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 名男生中随机抽取
名男生中随机抽取 名学生测量其身高,据测量被测学生的身高全部在
名学生测量其身高,据测量被测学生的身高全部在 到
到 之间.将测量结果按如下方式分成
之间.将测量结果按如下方式分成 组:第一组
组:第一组 ,第二组
,第二组 , ,第八组
, ,第八组 ,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.| 分组 | 频数 | 频率 | 频率/组距 |
| | | | |
 |  |  | 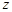 |
 |  |  |  |
| | | | |

 名男生,记他们的身高分别为
名男生,记他们的身高分别为 ,求满足:
,求满足: 的事件的概率.
的事件的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 )分成六段
)分成六段 ,
, ,
, ,
, ,
, ,
, 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图. 的车辆为
的车辆为 ,
, , ,
, , (
( 为车速在
为车速在 上的频数),车速在
上的频数),车速在 的车辆为
的车辆为 ,
, , ,
, , (
( 为车速在
为车速在 上的频数),从车速在
上的频数),从车速在 的车辆中任意抽取
的车辆中任意抽取 辆共有几种情况?请列举出所有的情况,并求抽取的
辆共有几种情况?请列举出所有的情况,并求抽取的 辆车的车速都在
辆车的车速都在 上的概率.
上的概率.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 射击环数 | 频数 | 频率 |
| 7 | 10 | 0.1 |
| 8 | 10 | 0.1 |
| 9 | x | 0.45 |
| 10 | 35 | y |
| 合计 | 100 | 1 |
| 射击环数 | 频数 | 频率 |
| 7 | 8 | 0.1 |
| 8 | 12 | 0.15 |
| 9 | z | |
| 10 | | 0.35 |
| 合计 | 80 | 1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
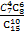 的是( )
的是( )| A.P(X=2) | B.P(X≤2) |
| C.P(X=4) | D.P(X≤4) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 排队人数 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com