
【题目】已知函数![]() .
.
(1)若函数![]() ,求
,求![]() 的极值;
的极值;
(2)证明:![]() .
.
(参考数据:![]()
![]()
![]()
![]() )
)
【答案】(1)见解析;(2)见证明
【解析】
(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;
(2)问题转化为证ex﹣x2﹣xlnx﹣1>0,根据xlnx≤x(x﹣1),问题转化为只需证明当x>0时,ex﹣2x2+x﹣1>0恒成立,令k(x)=ex﹣2x2+x﹣1,(x≥0),根据函数的单调性证明即可.
(1)![]() ,
,![]() ,当
,当![]() ,
,![]() ,
,
当![]() ,
,![]() ,
,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,![]() 在
在![]() 取得极大值,极大值为
取得极大值,极大值为![]() ,无极大值.
,无极大值.
(2)要证f(x)+1<ex﹣x2.
即证ex﹣x2﹣xlnx﹣1>0,
先证明lnx≤x﹣1,取h(x)=lnx﹣x+1,则h′(x)=![]() ,
,
易知h(x)在(0,1)递增,在(1,+∞)递减,
故h(x)≤h(1)=0,即lnx≤x﹣1,当且仅当x=1时取“=”,
故xlnx≤x(x﹣1),ex﹣x2﹣xlnx≥ex﹣2x2+x﹣1,
故只需证明当x>0时,ex﹣2x2+x﹣1>0恒成立,
令k(x)=ex﹣2x2+x﹣1,(x≥0),则k′(x)=ex﹣4x+1,
令F(x)=k′(x),则F′(x)=ex﹣4,令F′(x)=0,解得:x=2ln2,
∵F′(x)递增,故x∈(0,2ln2]时,F′(x)≤0,F(x)递减,即k′(x)递减,
x∈(2ln2,+∞)时,F′(x)>0,F(x)递增,即k′(x)递增,
且k′(2ln2)=5﹣8ln2<0,k′(0)=2>0,k′(2)=e2﹣8+1>0,
由零点存在定理,可知x1∈(0,2ln2),x2∈(2ln2,2),使得k′(x1)=k′(x2)=0,
故0<x<x1或x>x2时,k′(x)>0,k(x)递增,当x1<x<x2时,k′(x)<0,k(x)递减,故k(x)的最小值是k(0)=0或k(x2),由k′(x2)=0,得![]() =4x2﹣1,
=4x2﹣1,
k(x2)=![]() ﹣2
﹣2![]() +x2﹣1=﹣(x2﹣2)(2x2﹣1),∵x2∈(2ln2,2),∴k(x2)>0,
+x2﹣1=﹣(x2﹣2)(2x2﹣1),∵x2∈(2ln2,2),∴k(x2)>0,
故x>0时,k(x)>0,原不等式成立.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】擎天柱为了防止魔方落入霸天虎手中,打算用激光刀将其销毁.擎天柱使用的方法是:每次切割可将魔方分成两个体积之比为![]() 的六面体,每个六面体恰包含魔方的一个面,且任两次操作得到的截面在魔方中均有交点,而魔方的属性决定每次切割只能暂时将它割开,而无法分离,且只要它有
的六面体,每个六面体恰包含魔方的一个面,且任两次操作得到的截面在魔方中均有交点,而魔方的属性决定每次切割只能暂时将它割开,而无法分离,且只要它有![]() 的小正方体区域始终未被割到,就无法被销毁,证明:无论擎天柱切割多少次,均无法销毁魔方.
的小正方体区域始终未被割到,就无法被销毁,证明:无论擎天柱切割多少次,均无法销毁魔方.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为支援武汉的防疫,某医院职工踊跃报名,其中报名的医生18人,护士12人,医技6人,根据需要,从中抽取一个容量为n的样本参加救援队,若采用系统抽样和分层抽样,均不用剔除人员.当抽取n+1人时,若采用系统抽样,则需剔除1个报名人员,则抽取的救援人员为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年,新冠状肺炎疫情牵动每一个中国人的心,危难时刻众志成城,共克时艰,为疫区助力.福建省漳州市东山县共101个海鲜商家及个人为缓解武汉物质压力,募捐价值百万的海鲜输送武汉.东山岛,别称陵岛,形似蝴蝶亦称蝶岛,隶属于福建省漳州市东山县,是福建省第二大岛,中国第七大岛,介于厦门市和广东省汕头之间,东南是著名的闽南渔场和粤东渔场交汇处,因地理位置发展海产品养殖业具有得天独厚的优势.根据养殖规模与以往的养殖经验,某海鲜商家的海产品每只质量(克)在正常环境下服从正态分布![]() .
.
(1)随机购买10只该商家的海产品,求至少买到一只质量小于265克该海产品的概率;
(2)2020年该商家考虑增加先进养殖技术投入,该商家欲预测先进养殖技术投入为49千元时的年收益增量.现用以往的先进养殖技术投入![]() (千元)与年收益增量
(千元)与年收益增量![]() (千元).
(千元).![]() 的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线
的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近,且
的附近,且![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ,其中
,其中![]()
![]() .根据所给的统计量,求y关于x的回归方程,并预测先进养殖技术投入为49千元时的年收益增量.
.根据所给的统计量,求y关于x的回归方程,并预测先进养殖技术投入为49千元时的年收益增量.
附:若随机变量![]() ,则
,则![]()
![]() ;
;
对于一组数据![]()
![]()
![]()
![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为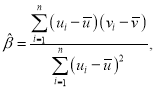
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次数学竞赛中,某些选手是朋友关系.记所有选手的集合为X,对集合X的子集Y,若可以将这些人两两分组,且每组中两名选手均是朋友关系,则称子集Y“可两两分组”.已知集合X不可两两分组,且对于任意选手![]() ,若A、B不是朋友关系,则
,若A、B不是朋友关系,则![]() 可两两分组,且X中没有一个人与其他所有人均为朋友关系证明:对任意选手
可两两分组,且X中没有一个人与其他所有人均为朋友关系证明:对任意选手![]() ,若a、b为朋友关系,b、c为朋友关系,则a、c也为朋友关系
,若a、b为朋友关系,b、c为朋友关系,则a、c也为朋友关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国在2018年社保又出新的好消息,之前流动就业人员跨地区就业后,社保转移接续的手续往往比较繁琐,费时费力.社保改革后将简化手续,深得流动就业人员的赞誉.某市社保局从2018年办理社保的人员中抽取300人,得到其办理手续所需时间(天)与人数的频数分布表:
时间 |
|
|
|
|
|
|
人数 | 15 | 60 | 90 | 75 | 45 | 15 |
(1)若300名办理社保的人员中流动人员210人,非流动人员90人,若办理时间超过4天的人员里非流动人员有60人,请完成办理社保手续所需时间与是否流动人员的列联表,并判断是否有95%的把握认为“办理社保手续所需时间与是否流动人员”有关.
列联表如下
流动人员 | 非流动人员 | 总计 | |
办理社保手续所需 时间不超过4天 | |||
办理社保手续所需 时间超过4天 | 60 | ||
总计 | 210 | 90 | 300 |
(2)为了改进工作作风,提高效率,从抽取的300人中办理时间为![]() 流动人员中利用分层抽样,抽取12名流动人员召开座谈会,其中3人要求交书面材料,3人中办理的时间为
流动人员中利用分层抽样,抽取12名流动人员召开座谈会,其中3人要求交书面材料,3人中办理的时间为![]() 的人数为
的人数为![]() ,求出
,求出![]() 分布列及期望值.
分布列及期望值.
附: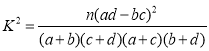
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com