
【题目】已知 ![]() =(sin2x,2cos2x﹣1),
=(sin2x,2cos2x﹣1), ![]() =(sinθ,cosθ)(0<θ<π),函数f(x)=
=(sinθ,cosθ)(0<θ<π),函数f(x)= ![]()
![]() 的图象经过点(
的图象经过点( ![]() ,1).
,1).
(1)求θ及f(x)的最小正周期;
(2)当x∈ ![]() 时,求f(x)的最大值和最小值.
时,求f(x)的最大值和最小值.
【答案】
(1)解:∵f(x)= ![]()
![]() =sin2xsinθ+cos2xcosθ=cos(2x﹣θ),
=sin2xsinθ+cos2xcosθ=cos(2x﹣θ),
∴f(x)的最小正周期为T=π,
∵y=f(x)的图象经过点( ![]() ,1),
,1),
∴cos( ![]() ﹣θ)=1,
﹣θ)=1,
又0<θ<π,
∴θ= ![]() ;
;
(2)解:由(1)得f(x)=cos(2x﹣ ![]() ),
),
∵﹣ ![]() ≤x≤
≤x≤ ![]() ,
,
∴﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤
≤ ![]() ,
,
当2x﹣ ![]() =0,即x=
=0,即x= ![]() 时,f(x)取得最大值1;
时,f(x)取得最大值1;
2x﹣ ![]() =﹣
=﹣ ![]() ,即x=﹣
,即x=﹣ ![]() 时,f(x)取得最小值﹣
时,f(x)取得最小值﹣ ![]()
【解析】(1)利用向量数量积的坐标运算易求f(x)=cos(2x﹣θ),从而可求f(x)的最小正周期;又y=f(x)的图象经过点( ![]() ,1),0<θ<π,可求得θ;(2)由(1)得f(x)=cos(2x﹣
,1),0<θ<π,可求得θ;(2)由(1)得f(x)=cos(2x﹣ ![]() ),﹣
),﹣ ![]() ≤x≤
≤x≤ ![]() ﹣
﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤
≤ ![]() ,利用余弦函数的单调性可求得f(x)的最大值和最小值.
,利用余弦函数的单调性可求得f(x)的最大值和最小值.
【考点精析】利用三角函数的最值对题目进行判断即可得到答案,需要熟知函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() +lnx,a∈R.
+lnx,a∈R.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若f(x)在区间(1,4)内单调递增,求a的取值范围;
(3)讨论函数g(x)=f′(x)﹣x的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线![]() 的参数方程为
的参数方程为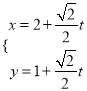 (
(![]() 为参数),圆
为参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列哪组中的函数f(x)与g(x)相等( )
A.f(x)=x2 , ![]()
B.f(x)=x+1,g(x)= ![]() +1
+1
C.f(x)=x,g(x)= ![]()
D.f(x)= ![]() ,g(x)=
,g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如图: 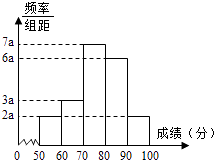
(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生任选2人,求此2人的成绩都在[60,70)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣1﹣x.
(1)若存在x∈[﹣1,ln ![]() ],满足a﹣ex+1+x<0成立,求实数a的取值范围.
],满足a﹣ex+1+x<0成立,求实数a的取值范围.
(2)当x≥0时,f(x)≥(t﹣1)x恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位组织职工去某地参观学习,需包车前往,甲车队说:“如果领队买一张全票,其余人可享受7折优惠。”乙车队说:“你们属于团体票,按原价的7.5折优惠。”这两个车队的原价、车型都是一样的,试根据单位去的人数比较两车队的收费哪家更优惠。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com