
【题目】如图,在四棱柱![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() .
.
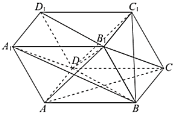
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() 是等边三角形,求二面角
是等边三角形,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)根据面面垂直的判定定理可知,只需证明![]() 平面
平面![]() 即可.
即可.
由![]() 为菱形可得
为菱形可得![]() ,连接
,连接![]() 和
和![]() 与
与![]() 的交点
的交点![]() ,
,
由等腰三角形性质可得![]() ,即能证得
,即能证得![]() 平面
平面![]() ;
;
(2)由题意知,![]() 平面
平面![]() ,可建立空间直角坐标系
,可建立空间直角坐标系![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,再分别求出平面
轴,再分别求出平面![]() 的法向量,平面
的法向量,平面![]() 的法向量,即可根据向量法求出二面角
的法向量,即可根据向量法求出二面角![]() 的余弦值.
的余弦值.
(1)如图,设![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,
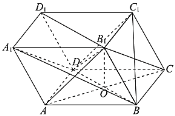
又![]() 为菱形,故
为菱形,故![]() ,
,![]() 为
为![]() 的中点.
的中点.
又![]() ,故
,故![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,
故![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)由![]() 是等边三角形,可得
是等边三角形,可得![]() ,故
,故![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,![]() 两两垂直.如图以
两两垂直.如图以![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
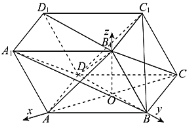
不妨设![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则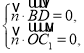 即
即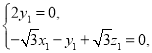 可取
可取![]() ,
,
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则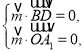 即
即 可取
可取![]() ,
,
所以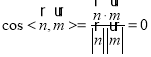 .
.
所以二面角![]() 的余弦值为0.
的余弦值为0.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】2019年末,武汉出现新型冠状病毒肺炎(![]() )疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户6口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为
)疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户6口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为![]() (
(![]() )且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为
)且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为![]() ,当
,当![]() 时,
时,![]() 最大,则
最大,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,直线
,直线![]() :
:![]() 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆![]() 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.![]() 为左顶点,过点
为左顶点,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点.
两点.

(1)求椭圆![]() 的方程;
的方程;
(2)以线段![]() 为直径的圆是否过定点?若是,写出所有定点的坐标;若不是,请说明理由.
为直径的圆是否过定点?若是,写出所有定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为多面体,平面
为多面体,平面![]() 与平面
与平面![]() 垂直,点
垂直,点![]() 在线段
在线段![]() 上,
上,![]()
![]() 都是正三角形.
都是正三角形.

(1)证明:直线![]() ∥面
∥面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值是
的余弦值是![]() ,若不存在请说明理由,若存在请求出
,若不存在请说明理由,若存在请求出![]() 点所在的位置。
点所在的位置。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,沿
的中点,沿![]() 将
将![]() 折起,使得点
折起,使得点![]() 到点
到点![]() 位置,且
位置,且![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 上的动点(与点
上的动点(与点![]() ,
,![]() 不重合).
不重合).
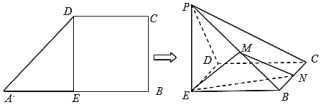
(Ⅰ)证明:平面![]() 平面
平面![]() 垂直;
垂直;
(Ⅱ)是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值
的余弦值![]() ?若存在,确定
?若存在,确定![]() 点位置;若不存在,说明理由.
点位置;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com