
分析 (Ⅰ)利用三角函数中的恒等变换应用化简函数解析式可得f(x)=$\frac{1}{2}$sin(2x-$\frac{π}{6}$)-$\frac{1}{4}$.结合A的范围及正弦函数的图象和性质即可得解.
(Ⅱ)由已知及(1)可求A,bc=1,利用余弦定理及向量的数量积可得$\overrightarrow{BA}$•$\overrightarrow{BC}$=c${\;}^{2}-\frac{1}{2}$.由$\left\{\begin{array}{l}{{a}^{2}+{c}^{2}>{b}^{2}}\\{{a}^{2}+{b}^{2}>{c}^{2}}\end{array}\right.$,又a2=b2+c2-1,可求$\left\{\begin{array}{l}{{b}^{2}>\frac{1}{2}}\\{{c}^{2}>\frac{1}{2}}\end{array}\right.$,从而解得范围.
解答 (本题满分为15分)
解:(Ⅰ)f(x)=cosxsin(x+$\frac{π}{6}$)-cos2x=cosx($\frac{\sqrt{3}}{2}$sinx+$\frac{1}{2}$cosx)-$\frac{1+cos2x}{2}$
=$\frac{\sqrt{3}}{4}$sin2x+$\frac{1}{4}$(1+cos2x)-$\frac{1+cos2x}{2}$=$\frac{\sqrt{3}}{4}$sin2x-$\frac{1}{4}$cos2x-$\frac{1}{4}$=$\frac{1}{2}$sin(2x-$\frac{π}{6}$)-$\frac{1}{4}$.--------------------------(4分)
因为是锐角三角形,所以A$∈(0,\frac{π}{2})$,所以2A-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{5π}{6}$),
所以sin(2A-$\frac{π}{6}$)∈(-$\frac{1}{2}$,1],所以f(A)∈(-$\frac{1}{2}$,$\frac{1}{4}$];----(7分)
(Ⅱ)因为f(A)=$\frac{1}{4}$,所以sin(2A-$\frac{π}{6}$)=1,又因为2A-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{5π}{6}$),
所以2A-$\frac{π}{6}$=$\frac{π}{2}$,即A=$\frac{π}{3}$.--------------------(8分)
又△ABC的面积为$\frac{\sqrt{3}}{4}$,所以bc=1.-------------------(9分)
$\overrightarrow{BA}$•$\overrightarrow{BC}$=accosB=ac×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2}$=$\frac{{b}^{2}+{c}^{2}-2bccosA+{c}^{2}-{b}^{2}}{2}$=c${\;}^{2}-\frac{1}{2}$.---------(11分)
因为△ABC为锐角三角形,所以$\left\{\begin{array}{l}{{a}^{2}+{c}^{2}>{b}^{2}}\\{{a}^{2}+{b}^{2}>{c}^{2}}\end{array}\right.$----------(12分)
又a2=b2+c2-1,所以$\left\{\begin{array}{l}{{b}^{2}>\frac{1}{2}}\\{{c}^{2}>\frac{1}{2}}\end{array}\right.$,
又bc=1,所以$\frac{1}{2}<{c}^{2}<2$,---------(14分)
故$\overrightarrow{BA}$•$\overrightarrow{BC}$的取值范围是(0,$\frac{3}{2}$).------------(15分)
(其它方法请酌情给分)
点评 本题主要考查了三角函数恒等变化的应用,考查了正弦定理,余弦定理,向量的数量积的运算等知识的综合应用,考查了正弦函数的图象和性质,综合性强,属于基本知识的考查.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平行四边形么BCD中,∠DAB=60°,AD=4,AB=2,将△CBD沿BD折起到△EBD的位置.
如图,在平行四边形么BCD中,∠DAB=60°,AD=4,AB=2,将△CBD沿BD折起到△EBD的位置.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
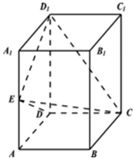 (Ⅰ)证明:A1B1∥平面CDE;
(Ⅰ)证明:A1B1∥平面CDE;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overline{z}$=-1-i | B. | |$\overline{z}$|=$\sqrt{2}$ | C. | |$\overline{z}$|=2 | D. | $\overline{z}$=-1+i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com