
【题目】某少数民族的刺绣有着悠久的历史,如图(1),(2),(3),(4)为最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形. 
(1)求出f(5)的值.
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式.
【答案】
(1)f(5)=41.
(2)因为f(2)-f(1)=4=4×1,
f(3)-f(2)=8=4×2,
f(4)-f(3)=12=4×3,
f(5)-f(4)=16=4×4,
…
由上式规律,所以得出f(n+1)-f(n)=4n.
因为f(n+1)-f(n)=4nf(n+1)=f(n)+4n
f(n)=f(n-1)+4(n-1)
=f(n-2)+4(n-1)+4(n-2)
=f(n-3)+4(n-1)+4(n-2)+4(n-3)
=…
=f(1)+4(n-1)+4(n-2)+4(n-3)+…+4
=2n2-2n+1.
【解析】找出第n+1项和第n项之间的关系,再利用数列中由递推数列推导通项数列的方法求f(n)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知α,β∈( ![]() ,π),且sinα+cosα=a,cos(β﹣α)=
,π),且sinα+cosα=a,cos(β﹣α)= ![]() .
.
(1)若a= ![]() ,求sinαcosα+tanα﹣
,求sinαcosα+tanα﹣ ![]() 的值;
的值;
(2)若a= ![]() ,求sinβ的值.
,求sinβ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某矩形花坛ABCD长AB=3m,宽AD=2m,现将此花坛在原有基础上有拓展成三角形区域,AB、AD分别延长至E、F并使E、C、F三点共线. 
(1)要使三角形AEF的面积大于16平方米,则AF的长应在什么范围内?
(2)当AF的长度是多少时,三角形AEF的面积最小?并求出最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】10.已知{an}是正数组成的数列,a1=1,且点( ![]() ,an+1)(n∈N*)在函数y=x2+1的图象上.
,an+1)(n∈N*)在函数y=x2+1的图象上.
(1)求数列{an}的通项公式.
(2)若数列{bn}满足b1=1,bn+1=bn+ ![]() ,求证:bn·bn+2<
,求证:bn·bn+2< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中心在坐标原点,焦点在坐标轴上,且经过
中心在坐标原点,焦点在坐标轴上,且经过![]() 三点.
三点.
(1)求椭圆![]() 的方程;
的方程;
(2)在直线![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,分别与椭圆
,分别与椭圆![]() 交于
交于![]() 两点,判断直线
两点,判断直线![]() 是否过定点?若是,求出该定点.若不是,请说明理由.
是否过定点?若是,求出该定点.若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为正方形,△ABE为等腰直角三角形,∠BAE=90°,且AD⊥AE. 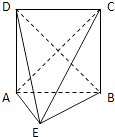
(1)证明:平面AEC⊥平面BED.
(2)求直线EC与平面BED所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com