分析:(1)根据等积法,可得三棱锥F-A1BC的体积VF-A1BC=VA1-FBC,根据已知中的数据,代入棱锥体积公式,可得答案.
(2)解法1:将侧面BCC1B1展开到侧面A1ACC1得到矩形ABB1A1,连结A1B,交C1C于点F,此时点F使得A1F+BF最小.此时F为C1C的中点.连接EF、AF,综合勾股定理,线面垂直的判定定理及性质,可得结论.
解法2:将侧面BCC1B1展开到侧面A1ACC1得到矩形ABB1A1,连结A1B,交C1C于点F,此时点F使得A1F+BF最小.此时FC平行且等于A1A的一半,过点C作CG⊥AB交AB于G,连接EF,
进而由线面垂直的判定定理及性质,可得结论.
解答: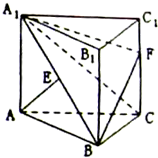
解:(1)因为侧面AA
1C
1C是边长为2的正方形,
∴AC=CC
1=2
∴BC=2
又∵
C1F=CF∴CF=∴
VF-A1BC=VA1-FBC=××2×××2=-------(5分)
(2)解法1:将侧面BCC
1B
1展开到侧面A
1ACC
1得到矩形ABB
1A
1,
连结A
1B,交C
1C于点F,此时点F使得A
1F+BF最小.此时F为C
1C的中点.-----------(7分)
连接EF、AF
在Rt△A
1AB中,AA
1=AB=2得
AE=在Rt△AFC中,AC=2,FC=1得
AF=在等腰△A
1FB中,
A1F=BF=得
EF=所以由
AE=,
AF=,
EF=得AE
2+EF
2=AF
2有勾股定理知AE⊥EF
∴
?AE⊥面A1FB?AE⊥A1F-----------------(12分)
解法2(参考给分):将侧面BCC
1B
1展开到侧面A
1ACC
1得到矩形ABB
1A
1,
连结A
1B,交C
1C于点F,
此时点F使得A
1F+BF最小.此时FC平行且等于A
1A的一半,
∴F为C
1C的中点.
过点C作CG⊥AB交AB于G,连接EF,
由FC∥EG且FC=EG知四边形EGCF为平行四边形
所以EF∥CG.
在正三棱柱ABC-A
1B
1C
1中知CG⊥面A
1AB,而EF∥CG,
所以EF⊥面A
1AB.
∴AE⊥EF
∴
?AE⊥面A1FB?AE⊥A1F 点评:本题考查的知识点是棱锥的体积公式,空间线面关系的判定,(1)的关键是利用等积法进行转化,(2)的关键是熟练掌握线面垂直的判定定理及性质

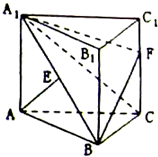 如图,正三棱柱ABC-A1B1C1中,侧面AA1C1C是边长为2的正方形,E是A1B的中点,F在棱CC1上.
如图,正三棱柱ABC-A1B1C1中,侧面AA1C1C是边长为2的正方形,E是A1B的中点,F在棱CC1上. 解:(1)因为侧面AA1C1C是边长为2的正方形,
解:(1)因为侧面AA1C1C是边长为2的正方形,

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.