
【题目】已知F1、F2分别为椭圆C: ![]() +
+ ![]() =1(a>b>0)的左、右焦点,且离心率为
=1(a>b>0)的左、右焦点,且离心率为 ![]() ,点A(﹣
,点A(﹣ ![]() ,
, ![]() )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的方程;
(2)是否存在斜率为k的直线l与椭圆C交于不同的两点M、N,使直线F2M与F2N的倾斜角互补,且直线l是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由.
【答案】
(1)解:∵F1、F2分别为椭圆C: ![]() +
+ ![]() =1(a>b>0)的左、右焦点,
=1(a>b>0)的左、右焦点,
且离心率为 ![]() ,点A(﹣
,点A(﹣ ![]() ,
, ![]() )在椭圆C上.
)在椭圆C上.
∴ 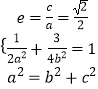 ,解得a2=2,b2=1.
,解得a2=2,b2=1.
∴椭圆C的方程为 ![]()
(2)解:由题意知直线MN存在斜率,其方程为y=kx+m,
由 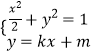 ,
,
消去y,得(2k2+1)x2+4kmx+2m2﹣2=0,
△=(4km)2﹣4(2k2+1)(2m2﹣2)>0,
设M( ![]() ,
, ![]() ,
,
又kF2M= ![]() ,
, ![]() ,
,
由已知直线F2M与F2N的倾斜角互补,
得 ![]() .
.
化简,得2kx1x2+(m﹣k)(x1+x2)﹣2m=0,
∴ ![]()
整理得m=﹣2k.
直线MN的方程为y=k(x﹣2),
因此直线MN过定点,该定点的坐标为(2,0).
【解析】(1)由已知得 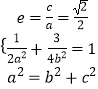 ,由此能求出椭圆C的方程.(2)由题意知直线MN存在斜率,其方程为y=kx+m,由
,由此能求出椭圆C的方程.(2)由题意知直线MN存在斜率,其方程为y=kx+m,由 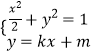 ,得(2k2+1)x2+4kmx+2m2﹣2=0,由此利用根的判别式和韦达定理结合已知条件推导出直线MN过定点(2,0).
,得(2k2+1)x2+4kmx+2m2﹣2=0,由此利用根的判别式和韦达定理结合已知条件推导出直线MN过定点(2,0).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.
(1)求曲线C的方程;
(2)是否存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有 ![]() <0?若存在,求出m的取值范围;若不存在,请说明理由.
<0?若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧面A1ADD1⊥底面ABCD,D1A=D1D= ![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点. 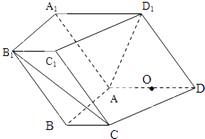
(1)求证:A1O∥平面AB1C;
(2)求锐二面角A﹣C1D1﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体ABCDE中,△ABC是正三角形,EA和DC都垂直于平面ABC,且EA=AB=2a,DC=a,F、G分别为EB和AB的中点. 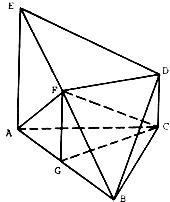
(1)求证:FD∥平面ABC;
(2)求二面角B﹣FC﹣G的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,倾斜角为 ![]() 的直线l与曲线C:
的直线l与曲线C: ![]() ,(α为参数)交于A,B两点,且|AB|=2,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,则直线l的极坐标方程是 .
,(α为参数)交于A,B两点,且|AB|=2,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,则直线l的极坐标方程是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公差不为零的等差数列{an}和等比数列{bn}中.已知a1=b1=1.a2=b2 . a6=b3
(1)求等差数列{an}的通项公式an和等比数列{bn}的通项公式bn;
(2)求数列{anbn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间四个点A(1,1,1),B(﹣4,0,2),C(﹣3,﹣1,0),D(﹣1,0,4),则直线AD与平面ABC所成的角为( )
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com