
【题目】如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:①EP⊥AC;②EP∥BD;③EP∥平面SBD;④EP⊥平面SAC,其中恒成立的为( )
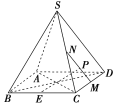
A.①③B.③④C.①②D.②③④
【答案】A
【解析】
在①中:由题意得 AC⊥平面SBD,从而平面EMN∥平面SBD,由此得到AC⊥EP;在②中:由异面直线的定义可知:EP与BD是异面直线;在③中:由平面EMN∥平面SBD,从而得到EP∥平面SBD;在④中:由已知得EM⊥平面SAC,从而得到EP与平面SAC不垂直.
如图所示,连接AC、BD相交于点O,连接EM,EN.
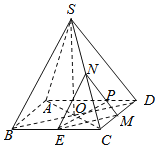
在①中:由正四棱锥S﹣ABCD,可得SO⊥底面ABCD,AC⊥BD,∴SO⊥AC.
∵SO∩BD=O,∴AC⊥平面SBD,∵E,M,N分别是BC,CD,SC的中点,
∴EM∥BD,MN∥SD,而EM∩MN=M,∴平面EMN∥平面SBD,
∴AC⊥平面EMN,∴AC⊥EP.故正确.
在②中:由异面直线的定义可知:EP与BD是异面直线,不可能EP∥BD,因此不正确;
在③中:由①可知平面EMN∥平面SBD,∴EP∥平面SBD,因此正确.
在④中:由①同理可得:EM⊥平面SAC,
若EP⊥平面SAC,则EP∥EM,与EP∩EM=E相矛盾,
因此当P与M不重合时,EP与平面SAC不垂直.即不正确.
∴恒成立的结论是:①③.
故选:A.


科目:高中数学 来源: 题型:
【题目】某乐园按时段收费,收费标准为:每玩一次不超过![]() 小时收费10元,超过
小时收费10元,超过![]() 小时的部分每小时收费
小时的部分每小时收费![]() 元(不足
元(不足![]() 小时的部分按
小时的部分按![]() 小时计算).现有甲、乙二人参与但都不超过
小时计算).现有甲、乙二人参与但都不超过![]() 小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
(1) 用![]() 表示甲乙玩都不超过
表示甲乙玩都不超过![]() 小时的付费情况,求甲、乙二人付费之和为44元的概率;
小时的付费情况,求甲、乙二人付费之和为44元的概率;
(2)抽奖活动的规则是:顾客通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数![]() ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-m|-|2x+3m|(m>0).
(1)当m=1时,求不等式f(x)≥1的解集;
(2)对于任意实数x,t,不等式f(x)<|2+t|+|t-1|恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
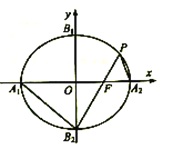
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的右焦点为
的右焦点为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() ,连结
,连结![]() 并延长交椭圆于点
并延长交椭圆于点![]() ,连结
,连结![]() ,
,![]() ,记椭圆
,记椭圆![]() 的离心率为
的离心率为![]() .
.
(1)若![]() ,
,![]() .
.
①求椭圆![]() 的标准方程;
的标准方程;
②求![]() 和
和![]() 的面积之比.
的面积之比.
(2)若直线![]() 和直线
和直线![]() 的斜率之积为
的斜率之积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面ABCD,侧棱
底面ABCD,侧棱![]() ,底面ABCD为直角梯形,其中
,底面ABCD为直角梯形,其中![]() ,
,![]() ,
,![]() ,O为AD中点.
,O为AD中点.

(1)求异面直线PB与CD所成角的余弦值;
(2)线段AD上是否存在点Q,使得它到平面PCD的距离为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在R上函数![]() ,有以下四个命题:
,有以下四个命题:
(1)直线![]() 与
与![]() 的图像的公共点个数一定为1;
的图像的公共点个数一定为1;
(2)若![]() 在区间
在区间![]() 上单调增函数,在
上单调增函数,在![]() 上也是单调增函数,则函数
上也是单调增函数,则函数![]() 在R上一定是单调增函数;
在R上一定是单调增函数;
(3)若![]() 为奇函数,则一定有
为奇函数,则一定有![]() ;
;
(4)若![]() ,则函数
,则函数![]() 一定不是偶函数.
一定不是偶函数.
其中正确的命题序号是_______.(请写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 的定义域为
的定义域为![]() ,对于定义域内的任意
,对于定义域内的任意![]() 存在实数
存在实数![]() 使得
使得![]() 成立,则称此函数具有“
成立,则称此函数具有“![]() 性质”.
性质”.
(1)判断函数![]() 是否具有“
是否具有“![]() 性质”,若具有“
性质”,若具有“![]() 性质”,写出所有
性质”,写出所有![]() 的值;若不具有“
的值;若不具有“![]() 性质”,请说明理由.
性质”,请说明理由.
(2)设函数![]() 具有“
具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,求当
,求当![]() 时函数
时函数![]() 的解析式;若
的解析式;若![]() 与
与![]()
![]() 交点个数为1001个,求
交点个数为1001个,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com