
【题目】以下是某地搜集到的新房屋的销售价格![]() 和房屋的面积
和房屋的面积![]() 的数据:
的数据:
房屋面积( | 115 | 110 | 80 | 135 | 105 |
销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为150![]() 时的销售价格.附:回归直线的斜率和截距的最小二乘法估计公式分别为:
时的销售价格.附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
, ![]()
科目:高中数学 来源: 题型:
【题目】定义:对于函数f(x),若在定义域内存在实数x,满足f(﹣x)=﹣f(x),则称f(x)为“局部奇函数”.
(1)已知二次函数f(x)=ax2+2x﹣4a(a∈R),试判断f(x)是否为定义域R上的“局部奇函数”?若是,求出满足f(﹣x)=﹣f(x)的x的值;若不是,请说明理由;
(2)若f(x)=2x+m是定义在区间[﹣1,1]上的“局部奇函数”,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将三颗骰子各掷一次,记事件A=“三个点数都不同”,B=“至少出现一个6点”,则条件概率P(A|B),P(B|A)分别是( )
A.![]() ,
, ![]()
B.![]() ,
, ![]()
C.![]() ,
, ![]()
D.![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax,(a∈R)
(1)若函数f(x)在点区间[e,+∞]处上为增函数,求a的取值范围;
(2)若函数f(x)的图象在点x=e(e为自然对数的底数)处的切线斜率为3,且k∈Z时,不等式 k(x﹣1)<f(x)在x∈(1,+∞)上恒成立,求k的最大值;
(3)n>m≥4时,证明:(mnn)m>(nmm)n .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0, ![]() )上的函数f(x)的导函数为f′(x),且对于任意的x∈(0,
)上的函数f(x)的导函数为f′(x),且对于任意的x∈(0, ![]() ),都有f′(x)sinx<f(x)cosx,则( )
),都有f′(x)sinx<f(x)cosx,则( )
A.![]() f(
f( ![]() )>
)> ![]() f(
f( ![]() )
)
B.f( ![]() )>f(1)
)>f(1)
C.![]() f(
f( ![]() )<f(
)<f( ![]() )
)
D.![]() f(
f( ![]() )<f(
)<f( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学(成绩得分为整数,满分100分)进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在![]() 的人数为12人.
的人数为12人.
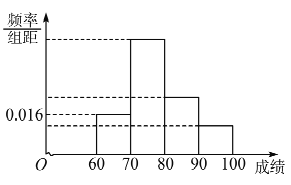
(Ⅰ)求此班级人数;
(Ⅱ)按规定预赛成绩不低于90分的选手参加决赛,已知甲乙两位选手已经取得决赛资格,参加决赛的选手按抽签方式决定出场顺序.
(i)甲不排在第一位乙不排在最后一位的概率;
(ii)记甲乙二人排在前三位的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:三棱锥![]() 中,侧面
中,侧面![]() 垂直底面,
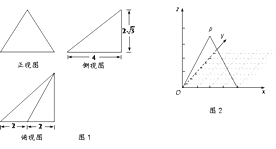
垂直底面, ![]() 是底面最长的边;图1是三棱锥
是底面最长的边;图1是三棱锥![]() 的三视图,其中的侧视图和俯视图均为直角三角形;图2是用斜二测画法画出的三棱锥
的三视图,其中的侧视图和俯视图均为直角三角形;图2是用斜二测画法画出的三棱锥![]() 的直观图的一部分,其中点
的直观图的一部分,其中点![]() 在
在![]() 平面内.
平面内.
(Ⅰ)请在图2中将三棱锥![]() 的直观图补充完整,并指出三棱锥
的直观图补充完整,并指出三棱锥![]() 的哪些面是直角三角形;
的哪些面是直角三角形;![]()
![]()
(Ⅱ)设二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值;
的值;
(Ⅲ)求点![]() 到面
到面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点
的两个焦点![]() ,动点
,动点![]() 在椭圆上,且使得
在椭圆上,且使得![]() 的点
的点![]() 恰有两个,动点
恰有两个,动点![]() 到焦点
到焦点![]() 的距离的最大值为
的距离的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)如图,以椭圆![]() 的长轴为直径作圆
的长轴为直径作圆![]() ,过直线
,过直线![]() 上的动点
上的动点![]() 作圆
作圆![]() 的两条切线,设切点分别为
的两条切线,设切点分别为![]() ,若直线
,若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com