
【题目】已知函数f(x)=ax3﹣x2+4x+3,若在区间[﹣2,1]上,f(x)≥0恒成立,则a的取值范围是( )
A.[﹣6,﹣2]
B.![]()
C.[﹣5,﹣3]
D.[﹣4,﹣3]
【答案】A
【解析】解:解:当x=0时,不等式ax3﹣x2+4x+3≥0对任意a∈R恒成立; 当0<x≤1时,ax3﹣x2+4x+3≥0可化为a≥ ![]()
![]() ,
,
令f(x)= ![]()
![]() ﹣
﹣ ![]() ,则f′(x)=﹣
,则f′(x)=﹣ ![]() +
+ ![]() =﹣
=﹣ ![]() (*),
(*),
当0<x≤1时,f′(x)>0,f(x)在(0,1]上单调递增,
f(x)max=f(1)=﹣6,∴a≥﹣6;
当﹣2≤x<0时,ax3﹣x2+4x+3≥0可化为a≤ ![]() ﹣
﹣ ![]() ,
,
由(*)式可知,当﹣2≤x<﹣1时,f′(x)<0,f(x)单调递减,
当﹣1<x<0时,f′(x)>0,f(x)单调递增,
f(x)min=f(﹣1)=﹣2,∴a≤﹣2;
综上所述,实数a的取值范围是﹣6≤a≤﹣2,即实数a的取值范围是[﹣6,﹣2].
所以答案是:[﹣6,﹣2].
【考点精析】根据题目的已知条件,利用函数单调性的判断方法和函数的最值及其几何意义的相关知识可以得到问题的答案,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若函数y=ax在区间[0,2]上的最大值和最小值的和为5,则函数y=logax在区间[ ![]() ,2]上的最大值和最小值之差是( )
,2]上的最大值和最小值之差是( )
A.1
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的参数方程为 ![]() (θ为参数),直线l经过点P(1,1),倾斜角
(θ为参数),直线l经过点P(1,1),倾斜角 ![]() ,
,
(1)写出直线l的参数方程;
(2)设l与圆C相交于两点A,B,求点P到A,B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线![]()
![]() 上有一点
上有一点![]() (
(![]() ),点
),点![]() 在
在![]() 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线![]() 的右焦点,过点
的右焦点,过点![]() 作双曲线
作双曲线![]() 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为![]() ,
, ![]() ,若平行四边形
,若平行四边形![]() 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. 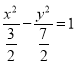
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数,
是奇函数,
(1)求a的值;
(2)试判断f(x)在(﹣∞,+∞)的单调性,并请你用函数单调性的定义给予证明;
(3)若对任意的t∈R,不等式f(mt2+1)+f(1﹣mt)<0恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xsinx,有下列四个结论: ①函数f(x)的图象关于y轴对称;
②存在常数T>0,对任意的实数x,恒有f(x+T)=f(x);
③对于任意给定的正数M,都存在实数x0 , 使得|f(x0)|≥M;
④函数f(x)在[0,π]上的最大值是 ![]() .
.
其中正确结论的序号是(请把所有正确结论的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是圆心为
是圆心为![]() 的圆
的圆![]() 上的动点,点
上的动点,点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)矩形![]() 的边所在直线与曲线
的边所在直线与曲线![]() 均相切,设矩形
均相切,设矩形![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com