
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”已知l丈为10尺,该楔体的三视图如图所示,其中网格纸上小正方形边长为1,则该楔体的体积为( )
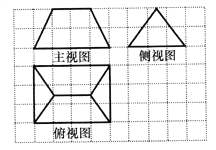
A. 10000立方尺 B. 11000立方尺
C. 12000立方尺 D. 13000立方尺
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.

(1)求异面直线BP与AC1所成角的余弦值;
(2)求直线CC1与平面AQC1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
,![]() 且
且![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 在直线
在直线![]() 上.
上.
(1)求椭圆的离心率;
(2)若![]() 的长轴长为
的长轴长为![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,问是否存在定点
两点,问是否存在定点![]() ,使得
,使得![]() ,
,![]() 的斜率之和为定值?若存在,求出所有满足条件的
的斜率之和为定值?若存在,求出所有满足条件的![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某保险公司的推销员中随机抽取50名,统计这些推销员某月的月销售额(单位:千元),由统计结果得如图频数分别表:
月销售额 分组 | [12.25,14.75) | [14.75,17.25) | [17.25,19.75) | [19.75,22.25) | [22.25,24.75) |
频数 | 4 | 10 | 24 | 8 | 4 |
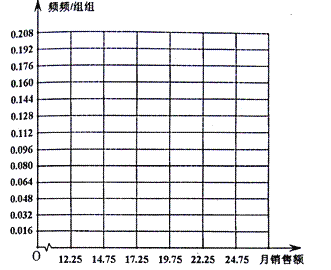
(1)作出这些数据的频率分布直方图;
(2)估计这些推销员的月销售额的平均数(同一组中的数据用该组区间的中点作代表);
(3)根据以上抽样调查数据,公司将推销员的月销售指标确定为17.875千元,试判断是否有60%的职工能够完成该销售指标.
查看答案和解析>>
科目:高中数学 来源: 题型:
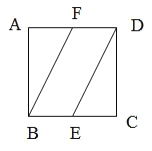
【题目】如图,在棱长为1正方体![]() 中,点
中,点![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 的中点,将
的中点,将![]() 沿
沿![]() 所在的直线进行翻折,将
所在的直线进行翻折,将![]() 沿
沿![]() 所在直线进行翻折,在翻折的过程中,下列说法错误的是( )
所在直线进行翻折,在翻折的过程中,下列说法错误的是( )
A. 无论旋转到什么位置,![]() 、
、![]() 两点都不可能重合
两点都不可能重合
B. 存在某个位置,使得直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
C. 存在某个位置,使得直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
D. 存在某个位置,使得直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
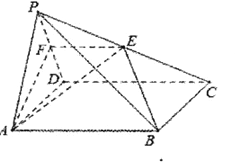
【题目】已知在四棱锥![]() 中,
中, ![]() 为正三角形,
为正三角形, ![]() ,底面
,底面![]() 为平行四边形,平面
为平行四边形,平面![]() 平面
平面![]() ,点
,点![]() 是侧棱
是侧棱![]() 的中点,平面
的中点,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
(1)求证: ![]() ;
;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角(锐角)的余弦值.
所成二面角(锐角)的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com