
【题目】如图所示,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
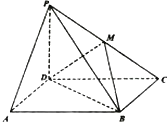
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数y=f(x),满足f(2)=0,函数y=f(x+1)的图象关于点(-1,0)中心对称,且对任意的负数x1,x2(x1≠x2),![]() 恒成立,则不等式f(x)<0的解集为____.
恒成立,则不等式f(x)<0的解集为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究“晚上喝绿茶与失眠”有无关系,调查了100名人士,得到下面的列联表:
失眠 | 不失眠 | 合计 | |
晚上喝绿茶 | 16 | 40 | 56 |
晚上不喝绿茶 | 5 | 39 | 44 |
合计 | 21 | 79 | 100 |
由已知数据可以求得:![]() ,则根据下面临界值表:
,则根据下面临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
可以做出的结论是( )
A. 在犯错误的概率不超过0.01的前提下认为“晚上喝绿茶与失眠有关”
B. 在犯错误的概率不超过0.01的前提下认为“晚上喝绿茶与失眠无关”
C. 在犯错误的概率不超过0.05的前提下认为“晚上喝绿茶与失眠有关”
D. 在犯错误的概率不超过0.05的前提下认为“晚上喝绿茶与失眠无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知抛物线y=x2+m的顶点M到直线l:![]() (t为参数)的距离为1
(t为参数)的距离为1
(Ⅰ)求m:
(Ⅱ)若直线l与抛物线相交于A,B两点,与y轴交于N点,求|S△MAN﹣S△MBN|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数exf(x)(e=2.71828…,是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质,下列函数:
①f(x)=![]() (x>1) ②f(x)=x2 ③f(x)=cosx ④f(x)=2-x
(x>1) ②f(x)=x2 ③f(x)=cosx ④f(x)=2-x
中具有M性质的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+![]() .
.
(I)当a=![]() 时,求函数f(x)在x=0处的切线方程;
时,求函数f(x)在x=0处的切线方程;
(II)函数f(x)是否存在零点?若存在,求出零点的个数;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂为检验车间一生产线是否工作正常,现从生产线中随机抽取一批零件样本,测量尺寸(单位: mm )绘成频率分布直方图如图所示:
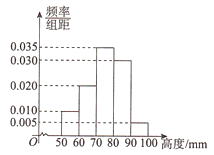
(Ⅰ)求该批零件样本尺寸的平均数 x 和样本方差 ![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)若该批零件尺寸![]() 服从正态分布
服从正态分布 ![]() ,其中
,其中 ![]() 近似为样本平均数
近似为样本平均数 ![]() 近似为样本方差
近似为样本方差 ![]() ,利用该正态分布求
,利用该正态分布求 ![]() ;
;
(Ⅲ)若从生产线中任取一零件,测量尺寸为30mm,根据 ![]() 原则判断该生产线是否正常?
原则判断该生产线是否正常?
附: ![]() ;若
;若![]() ,则
,则 ![]() ,
, ![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com