
ijѧ����֤���Ȳ�����ǰn���ʽʱ��֤�����£�
(1)��n=1ʱ��S1=a1��Ȼ������
(2)����n=kʱ����ʽ��������Sn=ka1+![]() ��
��
��n=k+1ʱ��
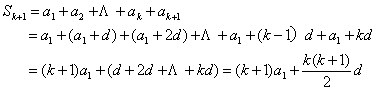
![]()
��n=k+1ʱ��ʽ������
����(1)��(2)֪����n��N����ʽ��������
����֤���������(����)
A.��nȡ��һ��ֵ1ʱ��֤������
B.���ɼ����д������
C.��n=k����n=k+1��������δ�ù��ɼ���
D.��n=k��n=k+1���������
 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ����ѧ������ ���ͣ�013
(1)��n=1ʱ��S1=a1��Ȼ������
(2)����n=kʱ����ʽ��������Sn=ka1+![]() ��
��
��n=k+1ʱ��
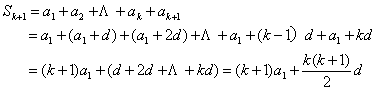
![]()
��n=k+1ʱ��ʽ������
����(1)��(2)֪����n��N����ʽ��������
����֤���������(����)
A.��nȡ��һ��ֵ1ʱ��֤������
B.���ɼ����д������
C.��n=k����n=k+1��������δ�ù��ɼ���
D.��n=k��n=k+1���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�013
��1����n=1ʱ��S1=a1��Ȼ����.
��2������n=kʱ����ʽ��������
Sk=ka1+![]() ��
��
��n=k+1ʱ��
Sk+1=a1+a2+��+ak+ak+1
=a1+(a1+d)+(a1+2d)+��+a1+(k-1)d+a1+kd
=(k+1)a1+(d+2d+��+kd)
=(k+1)a1+![]() d
d
=(k+1)a1+![]() d.
d.
��n=k+1ʱ��ʽ����.
���ɣ�1����2����֪��n��N+,��ʽ����.
����֤��������ǣ�������
A.��nȡ��һ��ֵ1ʱ��֤������
B.���ɼ���д������
C.��n=k��n=k+1��������δ�ù��ɼ���
D.��n=k��n=k+1���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ѡ����ѧ��4-5�˽�A�� �˽�A�� ���ͣ�013
ijѧ����֤���Ȳ�����ǰn���ʽʱ��֤�����£�
(1)��n��1ʱ��S1��a1��Ȼ������
(2)����n��kʱ����ʽ��������
Sk��ka1��![]() ��
��
��n��k��1ʱ��
Sk+1��a1��a2������ak��ak+1
��a1��(a1��d)��(a1��2d)������a1��(k��1)d��a1��kd
��(k��1)a1��(d��2d������kd)
��(k��1)a1��![]() d
d
��(k��1)a1��![]() d��
d��
��n��k��1ʱ��ʽ������
����(1)(2)��֪��n��N+����ʽ������
����֤���������
��nȡ��һ��ֵ1ʱ��֤������
���ɼ���д������
��n��k��n��k��1��������δ�ù��ɼ���
��n��k��n��k��1���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��1����n=1ʱ��S1=a1��Ȼ����.
��2������n=kʱ����ʽ��������
Sk=ka1+![]() ��
��
��n=k+1ʱ��
Sk+1=a1+a2+��+ak+ak+1
=a1+(a1+d)+(a1+2d)+��+a1+(k-1)d+a1+kd
=(k+1)a1+(d+2d+��+kd)
=(k+1)a1+![]() d
d
=(k+1)a1+![]() d.
d.
��n=k+1ʱ��ʽ����.
���ɣ�1����2����֪��n��N+,��ʽ����.
����֤��������ǣ� ��
A.��nȡ��һ��ֵ1ʱ��֤������
B.���ɼ���д������
C.��n=k��n=k+1��������δ�ù��ɼ���
D.��n=k��n=k+1���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
(1)��n=1ʱ��S1=a1��Ȼ������
(2)���赱n=kʱ����ʽ��������Sk=ka1+![]() ,
,
��n=k+1ʱ��Sk+1 =a1+a2+��+ak+ak+1 =a1+(a1+d)+(a1+2d)+��+��a1+(k-1)d��+(a1+kd)=(k+1)a1+(d+2d+��+kd)
=(k+1)a1+![]() d=(k+1)a1+
d=(k+1)a1+![]() d��
d��
��n=k+1ʱ��ʽ����.
��(1)(2)֪����n��N*ʱ����ʽ������.
����֤���������(����)
A.��nȡ��һ��ֵ1ʱ��֤������
B.���ɼ����д������
C.��n=k��n=k+1ʱ��������δ�ù��ɼ���
D.��n=k��n=k+1ʱ�������д���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com