
【题目】已知定义在区间[﹣3,3]上的单调函数f(x)满足:对任意的x∈[﹣3,3],都有f(f(x)﹣2x)=6,则在[﹣3,3]上随机取一个实数x,使得f(x)的值不小于4的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】公比为q(q≠1)的等比数列a1 , a2 , a3 , a4 , 若删去其中的某一项后,剩余的三项(不改变原有顺序)成等差数列,则所有满足条件的q的取值的代数和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() (ω>0)的图象与x轴正半轴交点的横坐标构成一个公差为
(ω>0)的图象与x轴正半轴交点的横坐标构成一个公差为 ![]() 的等差数列,若要得到函数g(x)=Asinωx的图象,只要将f(x)的图象( )个单位.
的等差数列,若要得到函数g(x)=Asinωx的图象,只要将f(x)的图象( )个单位.
A.向左平移 ![]()
B.向右平移 ![]()
C.向左平移 ![]()
D.向右平移 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科技公司生产一种手机加密芯片,其质量按测试指标划分为:指标大于或等于70为合格品,小于70为次品.现随机抽取这种芯片共120件进行检测,检测结果统计如表:
测试指标 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
芯片数量(件) | 8 | 22 | 45 | 37 | 8 |
已知生产一件芯片,若是合格品可盈利400元,若是次品则亏损50元.
(Ⅰ)试估计生产一件芯片为合格品的概率;并求生产3件芯片所获得的利润不少于700元的概率.
(Ⅱ)记ξ为生产4件芯片所得的总利润,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台DEF﹣ABC中,AB=2DE,G,H分别为AC,BC的中点.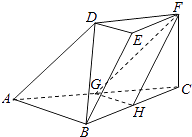
(Ⅰ)求证:BD∥平面FGH;
(Ⅱ)若CF⊥平面ABC,AB⊥BC,CF=DE,∠BAC=45°,求平面FGH与平面ACFD所成的角(锐角)的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上,点A、C为射线PM上的两点,点B、D为射线PN上的两点,则有 ![]() (其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有
(其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有 ![]() =(其中VP﹣ABE、VP﹣CDF分别为四面体P﹣ABE、P﹣CDF的体积).
=(其中VP﹣ABE、VP﹣CDF分别为四面体P﹣ABE、P﹣CDF的体积).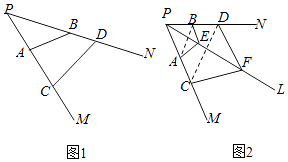
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y= ![]() 与y=ln(1﹣x)的定义域分别为M、N,则M∪N=( )
与y=ln(1﹣x)的定义域分别为M、N,则M∪N=( )
A.(1,2]
B.[1,2]
C.(﹣∞,1]∪(2,+∞)
D.(﹣∞,1)∪[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ﹣alnx.
﹣alnx.
(Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求函数y=f(x)的单调区间和极值;
(Ⅲ)若函数f(x)在区间(1,e2]内恰有两个零点,试求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com