Question

9．如图，在正方体ABCD-A₁B₁C₁D₁中，E、F分别为AD₁，CD₁中点．
（1）求异面直线EF与CD所成角的大小；
（2）求证：EF⊥平面BDD₁B₁．

Answer 1

分析 （1）连接AC，由EF∥AC，得∠ACD是异面直线EF与CD所成的角，求出这个角的大小即可；
（2）先证明AC⊥平面BDD₁B₁，再由EF∥AC证明EF⊥平面BDD₁B₁．

解答 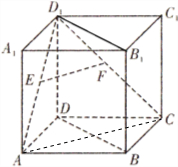解：（1）如图所示，连接AC，
∵E、F是AD₁，CD₁中点，
∴EF∥AC，
∴∠ACD是异面直线EF与CD所成的角，
又∵四边形ABCD是正方形，
∴∠ACD=45°；
即EF与CD所成的角是45°；
（2）证明：正方体ABCD-A₁B₁C₁D₁中，四边形ABCD是正方形，
∴AC⊥BD；
又BB₁⊥底面ABCD，
AC?平面ABCD，
∴BB₁⊥AC，
且BD∩BB₁=B，
BD?平面BDD₁B₁，
BB₁?平面BDD₁B₁，
∴AC⊥平面BDD₁B₁；
由（1）知，EF∥AC，
∴EF⊥平面BDD₁B₁．

点评 本题考查了求异面直线所成角的问题，也考查了空间中的平行与垂直关系的应用问题，是基础题目．