
(理)如图2,E、F分别是矩形ABCD的边AB、CD的中点,G是EF上的一点.
将△GAB、△GCB分别沿AB、CD翻折成△G1AB、△G2CD,并连结G1G2,使得平面G1AB⊥平面ABCD,G1G2//AD,且G1G2<AD. 连结BG2,如图3.
(Ⅰ)证明平面G1AB⊥平面G1ADG2;
(Ⅱ)当AB=12,BC=25,EG=8时,求直线BG2和平面G1ADG2所成的角.

(文)已知某质点的运动方程为 ,其运动轨迹的一部分如图所示.
,其运动轨迹的一部分如图所示.
|
(2)若当 恒成立,
恒成立,
求d的取值范围.
(理)解 解法一(I)因为平面G1AB⊥平面ABCD,平面G1AB∩平面ABCD=AB,
|
 平面ABCD,所以AD⊥平面G1AB. 又AD
平面ABCD,所以AD⊥平面G1AB. 又AD  平面G1ADG2,所以平面G1AB⊥平面G1ADG2.
平面G1ADG2,所以平面G1AB⊥平面G1ADG2.
(II)过点B作BH⊥AG1于点H,连结G2H,
由(I)的结论可知,BH⊥平面G1ADG2,
所以∠BG1H是BG2和平面G1ADG2所成的角.
因为平面G1AB⊥平面ABCD,
平面G1AB∩平面ABCD=AB,G1E=AB
G1E 平面G1AB,所以G1E⊥平面ABCD,故G1E⊥EF.
平面G1AB,所以G1E⊥平面ABCD,故G1E⊥EF.
因为G1G2<AD,AD=EF,所以可在EF上取一点O,使EO=G1G2,又因
|
由题设AB=12,BC=25,EG=8,则GF=17.
所以G2O=G1E=8,G2F=17,
OF=
因为AD⊥平面G1AB,G1G2//AD,
所以G1G2⊥平面G1AB,从而G1G2⊥G1B.
故BG =BE2+EG
=BE2+EG +G1G
+G1G =62+82+102=200,BG2=
=62+82+102=200,BG2= .
.
又AG1=
故
即直线BG2与平面G1ADG2所成的角是
解法二 (I)因为平面G1AB⊥平面ABCD,平面G1AB∩平面ABCD=AB,
G1E⊥AB,G1E 平面G1AB,所以G1E⊥平面ABCD,从而G1E⊥AD.
平面G1AB,所以G1E⊥平面ABCD,从而G1E⊥AD.
又AB⊥AD,所以AD⊥平面G1AB. 因为AD 平面G1ADG2,
平面G1ADG2,
所以平面G1AB⊥平面G1ADG2.
(II)由(I)可知,G1E⊥平面ABCD,故可以E为原点,分别以直线EB、EF、EG1,为x轴、y轴、z轴建立空间直角坐标系(如图).由题设AB=12,BC=25,EG=8,
则EB=6,EF=25,EG1=8,相关各点的坐标分别是A(-6,0,0),
D(-6,25,0),G1(0,0,8),B(6,0,0)
所以 .
.
设 的一个法向量,
的一个法向量,
由
过点G2作G2O⊥平面ABCD于点O,因为G2G=G2D,所以OC=OD,
于是点O在y轴上.
因为G1G2//AD,所以G1G2//EF,G2O=G1E=8.
设G2(0,m,8)(0<m<25),由172=82+(25-m)2解得m=10,
所以 =(0,10,8)-(6,0,0)=(-6,10,8).
=(0,10,8)-(6,0,0)=(-6,10,8).
设BG2和平面G1ADG2所成的有是θ,则

故直线BG2与平面G1ADG2所成的角是
(文) 解:(1)S′(t)=3t2+2bt+c,由图象可知,S(t)在t=1和t=3处取极值,
∴S′(1)=0,S′(3)=0,…………………………………………2分
即1,3,是方程3t2+2bt+c=0的两根,

(2)由(1)知,S′(t)=tt2+9t+d, S′(t)=3(t-1)(t-3).
当t∈[ ,1]时,S′(t)>0,当t∈(1,3)时,S′(t)<0,
,1]时,S′(t)>0,当t∈(1,3)时,S′(t)<0,
当t∈(3,4)时,S′(t)>0.
∴当t∈[ ,4]时,S(t)的最大值为4+d,…………………………9分
,4]时,S(t)的最大值为4+d,…………………………9分
S(t)<3d2在[ ,4]上恒成立的充要条件是4+d<3d2,
,4]上恒成立的充要条件是4+d<3d2,
∴解得d的取值范围是d> 或d<-1.………………………………12分
或d<-1.………………………………12分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
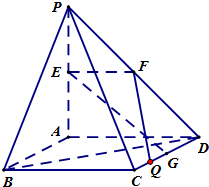 (理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.
(理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.| 4 |
| 5 |
| e |
| e |
| π |
| 2 |
| a |
| 1 |
| 2 |
| e |
| ||
| 2 |
| e |
| e |
| e |
| a |
| a |
| b |
| e |
| e |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (理)如图,四棱锥P-ABCD的底面是矩形,PA⊥面ABCD,PA=2
(理)如图,四棱锥P-ABCD的底面是矩形,PA⊥面ABCD,PA=2| 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•崇明县二模)(理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.
(2011•崇明县二模)(理)如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.| 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(04年湖南卷理)(12分)
如图,在底面是菱形的四棱锥![]() 中,
中,![]()
![]()
![]() ,点E在PD上,且PE:ED=2:1。
,点E在PD上,且PE:ED=2:1。
(Ⅰ)证明![]() ;
;
(Ⅱ)求以AC为棱,EAC与DAC为面的二面角![]() 的大小;
的大小;
(Ⅲ)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com