
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的极值;
的极值;
(2)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(3)若对任意的![]() ,
,![]() ,恒有
,恒有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)极小值![]() ,无极大值;(2)参考解析;(3)
,无极大值;(2)参考解析;(3)![]()
【解析】
试题分析:第一问,将![]() 代入
代入![]() 中确定函数
中确定函数![]() 的解析式,对
的解析式,对![]() 进行求导,判断
进行求导,判断![]() 的单调性,确定在
的单调性,确定在![]() 时,函数
时,函数![]() 有极小值,但无极大值,在解题过程中,注意函数的定义域;第二问,对
有极小值,但无极大值,在解题过程中,注意函数的定义域;第二问,对![]() 求导,
求导,![]() 的根为
的根为![]() 和
和![]() ,所以要判断函数
,所以要判断函数![]() 的单调性,需对
的单调性,需对![]() 和
和![]() 的大小进行3种情况的讨论;第三问,由第二问可知,当
的大小进行3种情况的讨论;第三问,由第二问可知,当![]() 时,
时,![]() 在
在![]() 为减函数,所以
为减函数,所以![]() 为最大值,
为最大值,![]() 为最小值,所以
为最小值,所以![]() 的最大值可以求出来,因为
的最大值可以求出来,因为![]() 对任意的
对任意的![]() 恒成立,所以
恒成立,所以![]() ,将
,将![]() 的最大值代入后,
的最大值代入后,![]() ,又是一个恒成立,整理表达式,即
,又是一个恒成立,整理表达式,即![]() 对任意
对任意![]() 恒成立,所以再求
恒成立,所以再求![]() 即可.
即可.
试题解析:(1)当![]() 时,
时,![]() 1分
1分
由![]() ,解得
,解得![]() . 2分
. 2分
∴![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数. 3分
上是增函数. 3分
∴![]() 的极小值为
的极小值为![]() ,无极大值. 4分
,无极大值. 4分
(2)![]() . 5分
. 5分
①当![]() 时,
时,![]() 在
在![]() 和
和![]() 上是减函数,在
上是减函数,在![]() 上是增函数; 6分
上是增函数; 6分
②当![]() 时,
时,![]() 在
在![]() 上是减函数; 8分
上是减函数; 8分
③当![]() 时,
时,![]() 在
在![]() 和
和![]() 上是减函数,在
上是减函数,在![]() 上是增函数. 8分
上是增函数. 8分
(3)当![]() 时,由(2)可知
时,由(2)可知![]() 在
在![]() 上是减函数,
上是减函数,
∴![]() . 9分
. 9分
由![]() 对任意的
对任意的![]() 恒成立,
恒成立,
∴![]() 10分
10分
即![]() 对任意
对任意![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立, 11分
恒成立, 11分
由于当![]() 时,
时,![]() ,∴
,∴![]() . 12分
. 12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}:1,﹣2,﹣2,3,3,3,﹣4,﹣4,﹣4,﹣4,…, ![]() ,…,即当
,…,即当 ![]() <n≤
<n≤ ![]() (k∈N*)时,
(k∈N*)时, ![]() .记Sn=a1+a2+…+an(n∈N).对于l∈N , 定义集合Pl=﹛n|Sn为an的整数倍,n∈N , 且1≤n≤l}
.记Sn=a1+a2+…+an(n∈N).对于l∈N , 定义集合Pl=﹛n|Sn为an的整数倍,n∈N , 且1≤n≤l}
(1)求P11中元素个数;
(2)求集合P2000中元素个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1 , V2 , V3 , V4 , 上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有( ) 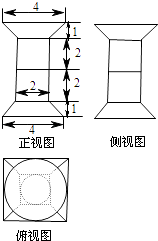
A.V1<V2<V4<V3
B.V1<V3<V2<V4
C.V2<V1<V3<V4
D.V2<V3<V1<V4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1 , C2的四个交点按纵坐标从大到小依次为A,B,C,D,记 ![]() ,△BDM和△ABN的面积分别为S1和S2 .
,△BDM和△ABN的面积分别为S1和S2 . 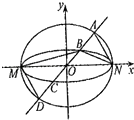
(1)当直线l与y轴重合时,若S1=λS2 , 求λ的值;
(2)当λ变化时,是否存在与坐标轴不重合的直线l,使得S1=λS2?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰直角三角形ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点, ![]() ,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′﹣BCDE,其中A′O=
,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′﹣BCDE,其中A′O= ![]() .
. 
(1)证明:A′O⊥平面BCDE;
(2)求二面角A′﹣CD﹣B的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图所示的程序框图,若输入的k=10,则该算法的功能是( ) 
A.计算数列{2n﹣1}的前10项和
B.计算数列{2n﹣1}的前9项和
C.计算数列{2n﹣1}的前10项和
D.计算数列{2n﹣1}的前9项和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测试中,卷面满分为100分,考生得分为整数,规定60分及以上为及格.某调研课题小组为了调查午休对考生复习效果的影响,对午休和不午休的考生进行了测试成绩的统计,数据如下表:
分数段 | 0~39 | 40~49 | 50~59 | 60~69 | 70~79 | 80~89 | 90~100 |
午休考生人数 | 29 | 34 | 37 | 29 | 23 | 18 | 10 |
不午休考生人数 | 20 | 52 | 68 | 30 | 15 | 12 | 3 |
(1)根据上述表格完成下列列联表:
及格人数 | 不及格人数 | 合计 | |
午休 | |||
不午休 | |||
合计 |
(2)判断“能否在犯错误的概率不超过0.010的前提下认为成绩及格与午休有关”?
| 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com