
【题目】已知函数f(x)=2x﹣3x2 , 设数列{an}满足:a1= ![]() ,an+1=f(an)
,an+1=f(an)
(1)求证:对任意的n∈N* , 都有0<an< ![]() ;
;
(2)求证: ![]() +
+ ![]() +…+
+…+ ![]() ≥4n+1﹣4.
≥4n+1﹣4.
【答案】
(1)证明:∵an+1=f(an),函数f(x)=2x﹣3x2,
∴an+1=2an﹣3 ![]() =﹣3
=﹣3 ![]() +
+ ![]() ≤
≤ ![]() .
.
若an+1= ![]() ,则an=
,则an= ![]() ,可得a1=
,可得a1= ![]() ,与已知a1=
,与已知a1= ![]() 矛盾,因此等号不成立.∴an<
矛盾,因此等号不成立.∴an< ![]() .
.
![]() =
= ![]() =
= ![]() =3an(3an﹣2)
=3an(3an﹣2) ![]() ,
,
由an< ![]() (n∈N*),可得an+1
(n∈N*),可得an+1 ![]() ,3an﹣2<0,因此an+1与an同号,a1=
,3an﹣2<0,因此an+1与an同号,a1= ![]() >0,∴an>0,
>0,∴an>0,
综上可得:对任意的n∈N*,都有0<an< ![]()
(2)解:∵0<an< ![]() ,an+1=2an﹣3
,an+1=2an﹣3 ![]() ,∴2 an+1﹣an=
,∴2 an+1﹣an= ![]() =an(1﹣3an)>0,
=an(1﹣3an)>0,
∴an+1>an,∴数列{an}单调递增.
∴n>1时, ![]() ,
,
∴ ![]() >4,
>4,
∴ ![]() =
= ![]() =
= ![]() >
> ![]() >
> ![]() >…>
>…> ![]() =4n+1,
=4n+1,
∴ ![]() +
+ ![]() +…+
+…+ ![]() ≥3(4+42+…+4n)=3×
≥3(4+42+…+4n)=3× ![]() =4n+1﹣4.
=4n+1﹣4.
∴ ![]() +
+ ![]() +…+
+…+ ![]() ≥4n+1﹣4
≥4n+1﹣4
【解析】1、由题意可得an+1=2an-3an2=-3(an-![]() )2 +
)2 +![]()
![]() ,可得
,可得![]() 做差an+1(an+1-
做差an+1(an+1-![]() )整理可得3an(3an﹣2) ( an
)整理可得3an(3an﹣2) ( an ![]() ) 2 由
) 2 由![]() (n
(n![]() N*) 可得an+1与an同号因此an>0.
N*) 可得an+1与an同号因此an>0.
2、由题意0<an< ![]() ,an+1=an﹣3 a n2 ,∴an+1﹣an= a n 3 a n 2=an(1﹣3an)>0,因此数列{an}单调递增n>1时,
,an+1=an﹣3 a n2 ,∴an+1﹣an= a n 3 a n 2=an(1﹣3an)>0,因此数列{an}单调递增n>1时, ![]() > a n >
> a n > ![]() ,
,
∴ ![]() >4,由递推公式可得式子
>4,由递推公式可得式子![]() 再由等比数列求和公式可得上式等于4n+1﹣4.即得结论。
再由等比数列求和公式可得上式等于4n+1﹣4.即得结论。
【考点精析】通过灵活运用数列的前n项和,掌握数列{an}的前n项和sn与通项an的关系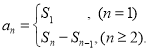 即可以解答此题.
即可以解答此题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(I)如果 ![]() 在
在 ![]() 处取得极值,求
处取得极值,求 ![]() 的值.
的值.
(II)求函数 ![]() 的单调区间.
的单调区间.
(III)当 ![]() 时,过点
时,过点 ![]() 存在函数曲线
存在函数曲线 ![]() 的切线,求
的切线,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(1+x)+alog2(1﹣x)(a∈R)的图象关于y轴对称.
(1)求函数f(x)的定义域;
(2)求a的值;
(3)若函数g(x)=x﹣2f(x)﹣2t有两个不同的零点,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() sin(2x+φ)(|φ|<
sin(2x+φ)(|φ|< ![]() )的图象关于直线x=
)的图象关于直线x= ![]() 对称,且当x1 , x2∈(﹣
对称,且当x1 , x2∈(﹣ ![]() ,﹣
,﹣ ![]() ),x1≠x2时,f(x1)=f(x2),则f(x1+x2)等于( )
),x1≠x2时,f(x1)=f(x2),则f(x1+x2)等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,摄影爱好者S在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为 ![]() .设S的眼睛到地面的距离为
.设S的眼睛到地面的距离为 ![]() 米
米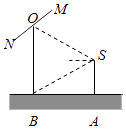
(1)求摄影爱好者到立柱的水平距离和立柱的高度;
(2)立柱的顶端有一长2米的彩杆MN绕其中点O在S与立柱所在的平面内旋转.摄影爱好者有一视角范围为 ![]() 的镜头,在彩杆转动的任意时刻,摄影爱好者是否都可以将彩杆全部摄入画面?请说明理由.
的镜头,在彩杆转动的任意时刻,摄影爱好者是否都可以将彩杆全部摄入画面?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图所示的程序框图,则该算法的功能是( ) 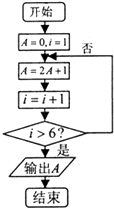
A.计算数列{2n﹣1}前5项的和
B.计算数列{2n﹣1}前5项的和
C.计算数列{2n﹣1}前6项的和
D.计算数列{2n﹣1}前6项的和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ ![]() +alnx.
+alnx.
(Ⅰ)若f(x)在区间[2,3]上单调递增,求实数a的取值范围;
(Ⅱ)设f(x)的导函数f′(x)的图象为曲线C,曲线C上的不同两点A(x1 , y1)、B(x2 , y2)所在直线的斜率为k,求证:当a≤4时,|k|>1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com