练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】“微信运动”是腾讯开发的一个记录跑步或行走情况(步数里程)的公众号用户通过该公众号可查看自己某时间段的运动情况.某人根据2018年1月至2018年11月期间每月离步的里程(单位:十公里)的数据绘制了下面的折线图.根据该折线图，下列结论正确的是( )

    A.月跑步里程逐月增加

    B.月跑步里程最大值出现在10月

    C.月跑步里程的中位数为5月份对应的里程数

    D.1月至5月的月跑步里程相对于6月至11月波动性更小，变化比较平稳

    【答案】BCD

    【解析】

    由对折线图数据的分析处理逐一检验选项即可得解．

    由折线图可知：月跑步里程逐月不是递增，故选项A错误；月跑步里程最大值出现在10月，故选项B正确；月跑步里程的中位数为5月份对应的里程数，故选项C正确；1月至5月的月跑步平均里程相对6月至11月，波动性更小、变化比较平稳，故选项正确.

    故选：B,C,．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，各个侧面均是边长为的正方形，为线段的中点.

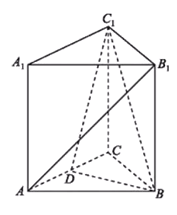
    (1)求证:直线平面；

    (2)求直线与平面所成角的余弦值；

    (3)设为线段上任意一点，在内的平面区域(包括边界)是否存在点，使，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2016年04月13日“山东济南非法经营疫苗系列案件”披露后，引发社会高度关注，引起公众、受种者和儿童家长对涉案疫苗安全性和有效性的担忧。为采取后续处置措施提供依据，保障受种者的健康，尽快恢复公众接种疫苗的信心,科学严谨地分析涉案疫苗接种给受种者带来的安全性风险和是否有效，对某疫苗预防疾病的效果，进行动物实验，得到下面表格中的统计数据：现从所有试验动物中任取一只，取到“注射疫苗”动物的概率为．

    未发病

    发病

    合计

    未注射疫苗

    注射疫苗

    合计

    （1）求列联表中的数据的值；

    （2）绘制发病率的条形统计图，并判断疫苗是否有效？

    （3）能够有多大把握认为疫苗有效？

    附：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直三棱柱ABC﹣A1B1C1中，AA1=AB=AC=2，D，E，F分别是B1A1 ， CC1 ， BC的中点，AE⊥A1B1 ， D为棱A1B1上的点．

    （1）证明：DF⊥AE；
    （2）求平面DEF与平面ABC所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，证明： 为偶函数；

    （2）若在上单调递增，求实数的取值范围；

    （3）若，求实数的取值范围，使在上恒成立.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】据相关规定，24小时内的降水量为日降水量（单位：mm），不同的日降水量对应的降水强度如表：

    日降水量

    （0，10）

    [10，25）

    [25，50）

    [50，100）

    [100，250）

    [250，+∞）

    降水强度

    小雨

    中雨

    大雨

    暴雨

    大暴雨

    特大暴雨

    为分析某市“主汛期”的降水情况，从该市2015年6月～8月有降水记录的监测数据中，随机抽取10天的数据作为样本，具体数据如下：
    16 12 23 65 24 37 39 21 36 68
    （1）请完成以如表示这组数据的茎叶图；

    （2）从样本中降水强度为大雨以上（含大雨）天气的5天中随机选取2天，求恰有1天是暴雨天气的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】据相关规定，24小时内的降水量为日降水量（单位：mm），不同的日降水量对应的降水强度如表：

    日降水量

    （0，10）

    [10，25）

    [25，50）

    [50，100）

    [100，250）

    [250，+∞）

    降水强度

    小雨

    中雨

    大雨

    暴雨

    大暴雨

    特大暴雨

    为分析某市“主汛期”的降水情况，从该市2015年6月～8月有降水记录的监测数据中，随机抽取10天的数据作为样本，具体数据如下：
    16 12 23 65 24 37 39 21 36 68
    （1）请完成以如表示这组数据的茎叶图；

    （2）从样本中降水强度为大雨以上（含大雨）天气的5天中随机选取2天，求恰有1天是暴雨天气的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正三棱锥P﹣ABC中E，F分别是AC，PC的中点，若EF⊥BF，AB=2，则三棱锥P﹣ABC的外接球的表面积（ ）
    A.4π
    B.6π
    C.8π
    D.12π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在梯形ABCD中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四边形ACFE为矩形，平面ACFE⊥平面ABCD，CF=1．
    （Ⅰ）求证：BC⊥平面ACFE；
    （Ⅱ）点M在线段EF上运动，设平面MAB与平面FCB所成二面角的平面角为θ（θ≤90°），试求cosθ的取值范围．

    查看答案和解析>>

    同步练习册答案