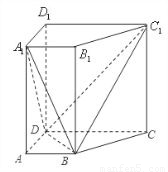
分析:(1)设E是DC的中点,连接BE,BD⊥BC,又BD⊥BB1,B1B∩BC=B,根据线面垂直的判定定理可知BD⊥平面BCC1B1;
(2)取DB的中点F,连接A1F,取DC1的中点M,连接FM,根据二面角的定义证得∠A1FM为二面角A1-BD-C1的平面角,取D1C1的中点H,连接A1H,HM,在Rt△A1HM中求出∠A1FM即可.
解答:解:(1)设E是DC的中点,连接BE,
则四边形DABE为正方形,∴BE⊥CD.故BD=
,BC=
,CD=2,
∴∠DBC=90°,即BD⊥BC.
又BD⊥BB
1,B
1B∩BC=B
∴BD⊥平面BCC
1B
1,(6分)
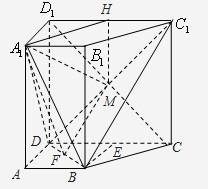
(2)由(I)知DB⊥平面BCC
1B
1,
又BC
1?平面BCC
1B
1,∴BD⊥BC
1,
取DB的中点F,连接A
1F,又A
1D=A
1B,
则A
1F⊥BD.取DC
1的中点M,连接FM,则FM∥BC
1,∴FM⊥BD.
∴∠A
1FM为二面角A
1-BD-C
1的平面角.
连接A
1M,在△A
1FM中,A
1F=
,
FM=
BC1=
=
,
取D
1C
1的中点H,连接A
1H,HM,在Rt△A
1HM中,
∵A
1H=
,HM=1,∴A
1M=
.
∴cos∠A
1FM=
.
∴二面角A
1-BD-C
1的余弦值为
.
点评:本题主要考查了直线与平面垂直,以及二面角等基础知识,考查空间想象能力、运算能力和推理论证能力,属于中档题.

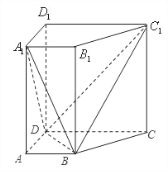 如图所示,已知直四棱柱ABCD-A1B1C1D1中,AD⊥DCAB∥DC,且满足
如图所示,已知直四棱柱ABCD-A1B1C1D1中,AD⊥DCAB∥DC,且满足 (2)由(I)知DB⊥平面BCC1B1,
(2)由(I)知DB⊥平面BCC1B1,

 中,
中,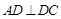 ,
,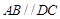 ,且满足
,且满足 .
. 平面
平面 ;
; 的余弦值.
的余弦值.