
【题目】袋中装有![]() 个大小相同的黑球和白球.已知从袋中任意摸出
个大小相同的黑球和白球.已知从袋中任意摸出![]() 个球,至少得到
个球,至少得到![]() 个白球的概率是
个白球的概率是![]() .
.
(1)求白球的个数;
(2)从袋中任意摸出![]() 个球,记得到白球的个数为
个球,记得到白球的个数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学一起去向老师询问各自的分班情况,老师说:你们四人中有![]() 位分到
位分到![]() 班,
班,![]() 位分到
位分到![]() 班,我现在给甲看乙、丙的班级,给乙看丙的班级,给丁看甲的班级.看后甲对大家说:我还是不知道我的班级,根据以上信息,则( )
班,我现在给甲看乙、丙的班级,给乙看丙的班级,给丁看甲的班级.看后甲对大家说:我还是不知道我的班级,根据以上信息,则( )
A. 乙可以知道四人的班级 B. 丁可以知道四人的班级
C. 乙、丁可以知道对方的班级 D. 乙、丁可以知道自己的班级
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD= ![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°. 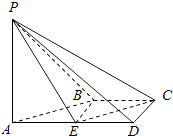
(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(2)若二面角P﹣CD﹣A的大小为45°,求直线PA与平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知边长为 ![]() 的菱形ABCD中,∠BAD=60°,沿对角线BD折成二面角A﹣BD﹣C为120°的四面体ABCD,则四面体的外接球的表面积为( )
的菱形ABCD中,∠BAD=60°,沿对角线BD折成二面角A﹣BD﹣C为120°的四面体ABCD,则四面体的外接球的表面积为( )
A.25π
B.26π
C.27π
D.28π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象过点
的图象过点![]() ,对任意
,对任意![]() 满足
满足![]() ,且有最小值为
,且有最小值为![]()
![]()
(1)求![]() 的解析式;
的解析式;
(2)求函数![]() 在区间[0,1]上的最小值,其中
在区间[0,1]上的最小值,其中![]() ;
;
(3)在区间[-1,3]上,![]() 的图象恒在函数
的图象恒在函数![]() 的图象上方,试确定实数
的图象上方,试确定实数![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①设有一个回归方程![]() ,变量
,变量![]() 增加一个单位时,
增加一个单位时,![]() 平均增加
平均增加![]() 个单位;②线性回归直线
个单位;②线性回归直线![]() 必过必过点
必过必过点![]() ;③在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有
;③在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有![]() 的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有
的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有![]() 的可能患肺病;其中错误的个数是( )
的可能患肺病;其中错误的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某批产品的销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为正常数).已知生产该批产品还需投入成本
为正常数).已知生产该批产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 元/件
元/件
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;(注:利润=销售收入-促销费-投入成本)
万元的函数;(注:利润=销售收入-促销费-投入成本)
(2)当促销费用投入多少万元时,该公司的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com