
【题目】某贫困地区有1500户居民,其中平原地区1050户,山区450户,为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元)
(I)应收集多少户山区家庭的样本数据?
(Ⅱ)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如果将频率率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
.如果将频率率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(Ⅲ)样本数据中,由5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有90%的把握认为“该地区2017年家庭年收入与地区有关”?
附:![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
超过2万元 | 不超过2万元 | 总计 | |
平原地区 | |||
山区 | 5 | ||
总计 |

【答案】(Ⅰ)45;(Ⅱ)0.45;(Ⅲ)答案见解析.
【解析】分析:(Ⅰ)由已知可得每户居民被抽取的概率为![]() ,根据古典概型概率公式可得结果;(Ⅱ)由直方图,利用符合条件矩形面积之和可求得该地区2017年家庭年收入超过
,根据古典概型概率公式可得结果;(Ⅱ)由直方图,利用符合条件矩形面积之和可求得该地区2017年家庭年收入超过![]() 万元的概率;(Ⅲ)样本数据中,年收入超过2万元的户数
万元的概率;(Ⅲ)样本数据中,年收入超过2万元的户数![]() 户,而样本数据中,有5户山区家庭的年收入超过2万元,完成列联表,求出
户,而样本数据中,有5户山区家庭的年收入超过2万元,完成列联表,求出![]() ,即可判断是否有
,即可判断是否有![]() 的把握认为 “该地区2017年家庭年收入与地区有关” .
的把握认为 “该地区2017年家庭年收入与地区有关” .
详解:(Ⅰ)由已知可得每户居民被抽取的概率为0.1,故应收集![]() 户山区家庭的样本数据.
户山区家庭的样本数据.
(Ⅱ)由直方图可知该地区2017年家庭年收入超过1.5万元的概率约为![]() .
.
(Ⅲ)样本数据中,年收入超过2万元的户数为![]() 户.
户.
而样本数据中,有5户山区家庭的年收入超过2万元,故列联表如下:
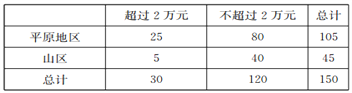
所以![]() ,
,
∴有![]() 的把握认为“该地区2017年家庭年收入与地区有关”.
的把握认为“该地区2017年家庭年收入与地区有关”.


科目:高中数学 来源: 题型:
【题目】为了对2016年某校中考成绩进行分析,在60分以上的全体同学中随机抽出8位,他们的数学分数(已折算为百分制)从小到大排是60、65、70、75、80、85、90、95,物理分数从小到大排是72、77、80、84、88、90、93、95. 参考公式:相关系数  ,
,
回归直线方程是: ![]() ,其中
,其中  ,
,
参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)若规定85分以上为优秀,求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率;
(2)若这8位同学的数学、物理、化学分数事实上对应如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
化学分数z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
①用变量y与x、z与x的相关系数说明物理与数学、化学与数学的相关程度;
②求y与x、z与x的线性回归方程(系数精确到0.01),当某同学的数学成绩为50分时,估计其物理、化学两科的得分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电脑公司有5名产品推销员,其工作年限与年推销金额的数据如表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
![]() 求年推销金额y关于工作年限x的线性回归方程;
求年推销金额y关于工作年限x的线性回归方程;
![]() 判断变量x与y之间是正相关还是负相关;
判断变量x与y之间是正相关还是负相关;
![]() 若第6名推销员的工作年限是11年,试估计他的年推销金额.
若第6名推销员的工作年限是11年,试估计他的年推销金额.
(参考数据![]() ,
,![]() ,
,
参考公式:线性回归方程![]() 中
中![]() ,
,![]() ,其中
,其中![]() 为样本平均数)
为样本平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinx+cosωx(ω>0)的图象与x轴交点的横坐标依次构成一个公差为
sinx+cosωx(ω>0)的图象与x轴交点的横坐标依次构成一个公差为 ![]() 的等差数列,把函数f(x)的图象沿x轴向左平移
的等差数列,把函数f(x)的图象沿x轴向左平移 ![]() 个单位,得到函数g(x)的图象,则( )
个单位,得到函数g(x)的图象,则( )
A.g(x)是奇函数
B.g(x)关于直线x=﹣ ![]() 对称
对称
C.g(x)在[ ![]() ,
, ![]() ]上是增函数
]上是增函数
D.当x∈[ ![]() ,
, ![]() ]时,g(x)的值域是[2,1]
]时,g(x)的值域是[2,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(1)求C;
(2)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期为π,且其图象向左平移
)的最小正周期为π,且其图象向左平移 ![]() 个单位后得到函数g(x)=cosωx的图象,则函数f(x)的图象( )
个单位后得到函数g(x)=cosωx的图象,则函数f(x)的图象( )
A.关于直线x= ![]() 对称
对称
B.关于直线x= ![]() 对称
对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com