
分析 (1)分别求出f(x)与g(x)的定义域确定出A与B,求出A与B补集的交集即可;
(2)表示出g(x)的定义域,根据A与B的交集,确定出m的值即可.
解答 解:(1)由函数f(x)=lg(x+1),得到x+1>0,
解得:x>-1,即A=(-1,+∞);
由函数g(x)=$\sqrt{2x+m-{x}^{2}}$及m=3,得到-x2+2x+3≥0,
整理得:x2-2x-3≤0,即(x-3)(x+1)≤0,
解得:-1≤x≤3,即B=[-1,3],
∴∁RB=(-∞,-1)∪(3,+∞),
则A∩(∁RB)=(3,+∞);
(2)由B中函数得:-x2+2x+m≥0,即x2-2x-m≤0,
∵A=(-1,+∞),A∩B=(-1,4],
∴x=4是方程x2-2x-m=0的解,
把x=4代入方程得:16-8-m=0,
解得:m=8.
点评 此题考查了交集及其运算,交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,4) | C. | (2,4) | D. | (4,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{9}$ | D. | $\frac{3}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在△ABC中,∠BAC=45°,∠ABC=60°,O为三角形的外心,以线段OB,OC为邻边作平行四边形,第四个顶点为D,再以OA,OD为邻边作平行四边形,它的第四个顶点为H.
在△ABC中,∠BAC=45°,∠ABC=60°,O为三角形的外心,以线段OB,OC为邻边作平行四边形,第四个顶点为D,再以OA,OD为邻边作平行四边形,它的第四个顶点为H.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
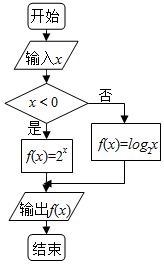 如图程序框图运行后,如果输出的函数值在区间[-2,$\frac{1}{2}$]内,则输入的实数x的取值范围是(-∞,-1]∪[$\frac{1}{4}$,$\sqrt{2}$].
如图程序框图运行后,如果输出的函数值在区间[-2,$\frac{1}{2}$]内,则输入的实数x的取值范围是(-∞,-1]∪[$\frac{1}{4}$,$\sqrt{2}$].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com