
【题目】如图,在三棱柱![]() 中,
中,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ,
,![]() 为
为![]() 的中点,且
的中点,且![]() ⊥
⊥![]() .
.
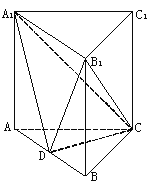
(1)求证:![]() ⊥平面
⊥平面![]() ;(2)求三棱锥
;(2)求三棱锥![]() 的体积.
的体积.
【答案】解:(1)见解析;(2)![]() =
=![]()
![]() ·CD
·CD
=![]() A1B1×B1B×CD=
A1B1×B1B×CD=![]() ×2
×2![]() ×2×
×2×![]() =
=![]() .
.
【解析】
本题考查线线垂直,线面垂直及多面体的体积的求法技巧,转化思想的应用,考查计算能力
(1)证明CD⊥BB1,通过BB1⊥AB,AB∩CD=D,即可证明BB1⊥面ABC
(2)所求的体积进行等价转化可以知道几何体的体积.
解:(1)∵AC=BC,D为AB的中点,∴CD⊥AB,又∵CD⊥DA1,∴CD⊥平面ABB1A1,∴CD⊥BB1,
又BB1⊥AB,AB∩CD=D,∴BB1⊥平面ABC
(2)由(1)知CD⊥平面AA1B1B,故CD是三棱锥C-A1B1D的高,
在Rt△ACB中,AC=BC=2,∴AB=2![]() ,CD=
,CD=![]() ,
,
又BB1=2,∴![]() =
=![]()
![]() ·CD
·CD
=![]() A1B1×B1B×CD=
A1B1×B1B×CD=![]() ×2
×2![]() ×2×
×2×![]() =
=![]()
请在此输入详解!


科目:高中数学 来源: 题型:
【题目】以下四个命题:
①“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
②“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
③若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
④对于命题![]() :
:![]() ,
,![]() ,则
,则![]() 为:
为:![]() ,
,![]()
其中真命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解高一年级学生学习数学的状态,从期中考试成绩中随机抽取50名学生的数学成绩,按成绩分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
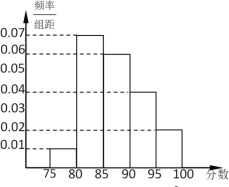
(1)由频率分布直方图,估计这50名学生数学成绩的中位数和平均数(保留到0.01);
(2)该校高一年级共有1000名学生,若本次考试成绩90分以上(含90分)为“优秀”等次,则根据频率分布直方图估计该校高一学生数学成绩达到“优秀”等次的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两地生产同一种瓷器,现从两地的瓷器中随机抽取了一共300件统计质量指标值,得到如图的两个统计图,其中甲地瓷器的质量指标值在区间![]() 和
和![]() 的频数相等.
的频数相等.

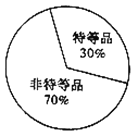
甲地瓷器质量频率分布直方图 乙地瓷器质量扇形统计图
(1)求直方图中![]() 的值,并估计甲地瓷器质量指标值的平均值;(同一组中的数据用区间的中点值作代表)
的值,并估计甲地瓷器质量指标值的平均值;(同一组中的数据用区间的中点值作代表)
(2)规定该种瓷器的质量指标值不低于125为特等品,且已知样本中甲地的特等品比乙地的特等品多10个,结合乙地瓷器质量扇形统计图完成下面的![]() 列联表,并判断是否有95%的把握认为甲、乙两地的瓷器质量有差异?
列联表,并判断是否有95%的把握认为甲、乙两地的瓷器质量有差异?
物等品 | 非特等品 | 合计 | |
甲地 | |||
乙地 | |||
合计 |
附: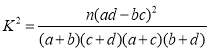 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】3个红球与3个黑球随机排成一行,从左到右依次在球上标记1,2,3,4,5,6,则红球上的数字之和小于黑球上的数字之和的概率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际羽毛球比赛规则从2006年5月开始,正式决定实行21分的比赛规则和每球得分制,并且每次得分者发球,所有单项的每局获胜分至少是21分,最高不超过30分,即先到21分的获胜一方赢得该局比赛,如果双方比分为![]() 时,获胜的一方需超过对方2分才算取胜,直至双方比分打成
时,获胜的一方需超过对方2分才算取胜,直至双方比分打成![]() 时,那么先到第30分的一方获胜.在一局比赛中,甲发球赢球的概率为
时,那么先到第30分的一方获胜.在一局比赛中,甲发球赢球的概率为![]() ,甲接发球贏球的概率为
,甲接发球贏球的概率为![]() ,则在比分为
,则在比分为![]() ,且甲发球的情况下,甲以
,且甲发球的情况下,甲以![]() 赢下比赛的概率为( )
赢下比赛的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
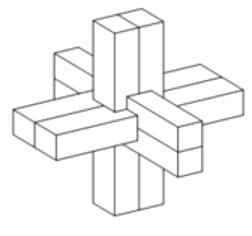
【题目】鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,从外表上看,六根等长的正四棱柱分成三组,经![]() 榫卯起来,如图,若正四棱柱的高为
榫卯起来,如图,若正四棱柱的高为![]() ,底面正方形的边长为
,底面正方形的边长为![]() ,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为( )(容器壁的厚度忽略不计)
,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为( )(容器壁的厚度忽略不计)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,且
,且![]() 对一切
对一切![]() 都成立.
都成立.
(1)当![]() 时.
时.
①求数列![]() 的通项公式;
的通项公式;
②若![]() ,求数列
,求数列![]() 的前
的前![]() 项的和
项的和![]() ;
;
(2)是否存在实数![]() ,使数列
,使数列![]() 是等差数列.如果存在,求出
是等差数列.如果存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com