
·ÖĪö £Ø1£©øł¾ŻČż½ĒŠĪĻąĖʵƵ½$\frac{DE}{AD}$=$\frac{BE}{AC}$£¬µĆµ½AE+DE=4£¬¹ŹEA+EB=4ŹĒ¶ØÖµ£¬
£Ø2£©Éč³öÖ±Ļß·½³Ģ£¬ĮŖĮ¢·½³Ģ×飬Ēó³öx1+1=$\frac{{9k}^{2}-4\sqrt{3}k}{{4k}^{2}+1}$£¬x2+1=$\frac{{9k}^{2}+4\sqrt{3}k}{{4k}^{2}+1}$£¬øł¾Ży1-y2=k£Øx1-1£©+k£Øx2-1£©£¬Ēó³öÖ±ĻßABµÄŠ±ĀŹŹĒ¶ØÖµ¼“æÉ£®
½ā“š £Ø1£©Ö¤Ć÷£ŗ”ßBE”ĪAC£¬”ą”÷BDE”×”÷CAD£¬
”ą$\frac{DE}{AD}$=$\frac{BE}{AC}$£¬”ßAD=AC=4£¬”ąDE=BE£¬”ßAE+DE=4£¬
¹Ź|EA|+|EB|=4ŹĒ¶ØÖµ£¬
ÓÉĶÖŌ²µÄ¶ØŅåµĆ£ŗ$\frac{{x}^{2}}{4}$+y2=1£¬£Øy”Ł0£©£»
£Ø2£©½ā£ŗÉčA£Øx1£¬y1£©£¬B£Øx2£¬y2£©£¬
Ö±ĻßMAµÄ·½³ĢŹĒy=k£Øx-1£©+$\frac{\sqrt{3}}{2}$£¬
Ö±ĻßMBµÄ·½³ĢŹĒy=-k£Øx-1£©+$\frac{\sqrt{3}}{2}$£¬
¹Ź$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}{+y}^{2}=1}\\{y=k£Øx-1£©+\frac{\sqrt{3}}{2}}\end{array}\right.$£¬ĻūČ„yµĆ£ŗ
£Ø4k2+1£©x2+£Ø4$\sqrt{3}$k-8k2£©x+4k2-4$\sqrt{3}$k-1=0£¬
x1=1£¬x2-1=-$\frac{4\sqrt{3}k+2}{{4k}^{2}+1}$£¬
¹Źy1-y2=k£Øx1-1£©+k£Øx2-1£©£¬
ŌņÖ±ĻßABµÄŠ±ĀŹKAB=$\frac{{y}_{2}{-y}_{1}}{{{x}_{2}-x}_{1}}$=$\frac{-4k}{-9\sqrt{3}k}$=$\frac{\sqrt{3}}{6}$£®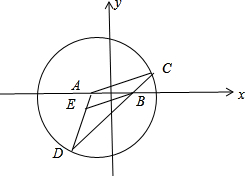
µćĘĄ ±¾Ģāæ¼²éĮĖÖ±Ļß·½³Ģ”¢ĶÖŌ²µÄ·½³ĢĪŹĢā£¬æ¼²éÖ±ĻßŗĶĶÖŌ²µÄ¹ŲĻµ£¬ŹōÓŚŃ¹ÖįĢā£®


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -2£¬-1£¬0£¬1£¬2£¬3 | B£® | 0£¬1£¬2£¬3 | C£® | 0£¬1£¬2 | D£® | 1£¬2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
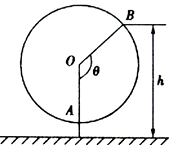 ČēĶ¼ŹĒŅ»øöĄĀ³µŹ¾ŅāĶ¼£¬øĆĄĀ³µµÄ°ė¾¶ĪŖ4.8m£¬Ō²ÉĻ×īµĶµćÓėµŲĆęµÄ¾ąĄėĪŖ0.8m£¬ĄĀ³µĆæ60s×Ŗ¶ÆŅ»Č¦£¬Ķ¼ÖŠOAÓėµŲĆę“¹Ö±£¬ŅŌOAĪŖŹ¼±ß£¬ÄꏱÕė×Ŗ¶Æ¦Č½Ēµ½OB£¬ÉčBµćÓėµŲĆęµÄ¾ąĄėĪŖhm£®
ČēĶ¼ŹĒŅ»øöĄĀ³µŹ¾ŅāĶ¼£¬øĆĄĀ³µµÄ°ė¾¶ĪŖ4.8m£¬Ō²ÉĻ×īµĶµćÓėµŲĆęµÄ¾ąĄėĪŖ0.8m£¬ĄĀ³µĆæ60s×Ŗ¶ÆŅ»Č¦£¬Ķ¼ÖŠOAÓėµŲĆę“¹Ö±£¬ŅŌOAĪŖŹ¼±ß£¬ÄꏱÕė×Ŗ¶Æ¦Č½Ēµ½OB£¬ÉčBµćÓėµŲĆęµÄ¾ąĄėĪŖhm£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | f£Øx£©ÓŠ¼«Öµ | B£® | f£Øx£©ÓŠĮćµć | C£® | f£Øx£©ŹĒĘęŗÆŹż | D£® | f£Øx£©ŹĒŌöŗÆŹż |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -$\frac{1}{2}$+$\frac{3}{2}$i | B£® | -$\frac{1}{2}$-$\frac{3}{2}$i | C£® | -1+3i | D£® | -1-3i |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 Ä³ÖŠŃ§Ń”Č”20ĆūÓÅŠćĶ¬Ń§²Ī¼Ó2016ÄźŹżŃ§Ó¦ÓĆÖŖŹ¶¾ŗČü£¬½«ĖūĆĒµÄ³É¼Ø£Ø°Ł·ÖÖĘ£¬¾łĪŖÕūŹż£©·Ö³É[40£¬50£©£¬[50£¬60£©£¬[60£¬70£©£¬[70£¬80£©£¬[80£¬90£©£¬[90£¬100]£¬¹²6×éŗó£¬µĆµ½ĘµĀŹ·Ö²¼Ö±·½Ķ¼£ØČēĶ¼£©£¬øł¾ŻĶ¼ÖŠµÄŠÅĻ¢£¬»Ų“šĻĀĮŠĪŹĢā£®
Ä³ÖŠŃ§Ń”Č”20ĆūÓÅŠćĶ¬Ń§²Ī¼Ó2016ÄźŹżŃ§Ó¦ÓĆÖŖŹ¶¾ŗČü£¬½«ĖūĆĒµÄ³É¼Ø£Ø°Ł·ÖÖĘ£¬¾łĪŖÕūŹż£©·Ö³É[40£¬50£©£¬[50£¬60£©£¬[60£¬70£©£¬[70£¬80£©£¬[80£¬90£©£¬[90£¬100]£¬¹²6×éŗó£¬µĆµ½ĘµĀŹ·Ö²¼Ö±·½Ķ¼£ØČēĶ¼£©£¬øł¾ŻĶ¼ÖŠµÄŠÅĻ¢£¬»Ų“šĻĀĮŠĪŹĢā£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com