
 的图象关于直线y=x对称.
的图象关于直线y=x对称. x互为反函数,它们的图象关于直线y=x对称,说明③正确.
x互为反函数,它们的图象关于直线y=x对称,说明③正确.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| ? |
| y |
. |
| x |
. |
| y |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省韶关市高三调研测试文科数学试卷(解析版) 题型:填空题
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为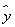 =0.85x-85.71,给定下列结论:
=0.85x-85.71,给定下列结论:
①y与x具有正的线性相关关系;
②回归直线过样本点的中心( ,
, );
);
③若该大学某女生身高增加1cm,则其体重约增加0.85kg;
④若该大学某女生身高为170cm,则可断定其体重必为58.79kg.
其中正确的结论是 .
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省蚌埠二中高二(上)期中数学试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省蚌埠二中高二(上)期中数学试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com